Kategori: Talteori

Selv om det kan være meget vanskeligt at faktorisere et stort tal m, så kan man alligevel godt afgøre om et givet tal m er et primtal.

Det lyser måske mærkeligt. Men vi kan jo også let afgøre om en dør er låst, uden at låse den op. Vi behøver ikke engang have en nøgle til låsen, det er bare at tage i håndtaget, så kan vi se om den er låst.

Der er forskellige primtalstests. Vi er allerede stødt på en metode; vi kan nemlig bruge Fermats lille sætning: Er p et primtal, og er a er helt tal som p ikke går op i, så vil

 \( a^{p-1} \equiv_p 1 \)

Her har jeg skrevet \(\equiv_p\) fordi vi regner modulo p.

Er a derfor et helt tal, mindre end primtallet p, så skal \(a^{p-1}\) være kongruent med 1, når vi regner modulo p. Det er her primtalstesten kommer ind i billedet. Hvis \(a^{p-1}\) nemlig ikke er kongruent med 1, modulo p, så er p ikke et primtal!

Vi ved at tallet p = 11 er et primtal. Vi kan let beregne \(1^{p-1}\), \(2^{p-1}\), \(3^{p-1}\), …, \(10^{p-1}\) modulo p:

a	1	2	3	4	5	6	7	8	9	10
\(a^{10}\)	1	1	1	1	1	1	1	1	1	1

Da tallet 11 er et primtal, så får vi lutter 1-taller.

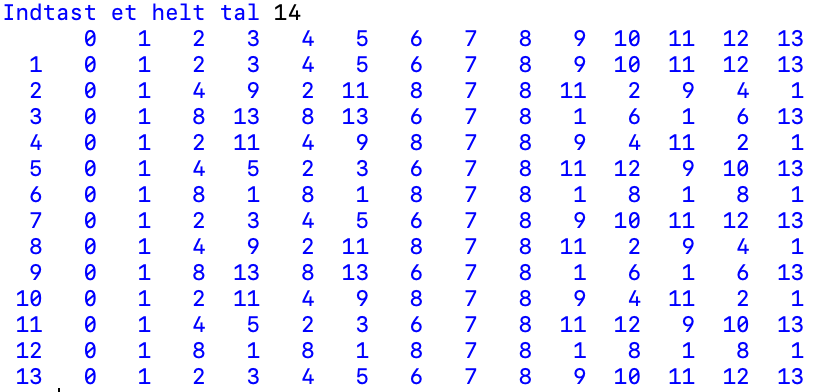
Vi ved også at tallet 15 ikke er et primtal. Vi kan tage hvert af de hele tal 1, 2, 3, …, 14, og opløfte dem i 14. potens. Hvis tallet 15 var et primtal, så skulle alle 14. potenser af tallene 1, 2, 3, …, 14 give 1, modulo 15:

a	1	2	3	4	5	6	7	8	9	10	11	12	13	14
\(a^{10}\)	1	4	9	1	10	6	4	4	6	10	1	9	4	1

Vi ser, at vi kun sjældent for et 1’tal, når vi opløfter hvert af tallene 1, 2, 3, …, 14 i 14. potens, og regner modulo 15. Der er dog enkelte 1-taller.

Når vi skal undersøge om et stort tal m er et primtal, så kan vi altså opløfte forskellige hele tal a, der er mindre end m, i m-1’te potens. Hvis bare en af disse beregninger givet et tal som ikke er er kongruent med 1, modulo m, så er m ikke et primtal.

Lad og se på tallet 129. Jeg ved ikke om det er et primtal. Lad og vælge forskellige hele tal a, der er mindre end 129, og opløfte dem i den 128. potens. Lad os begynde med de små hele tal:

a	1	2	3	4	5	6
\(a^{128}\)	1	4	9	16	25	36

Vi ser ret hurtigt at vi ikke kun får 1-taller, når vi regner modulo 129. Dermed er tallet 129 ikke et primtal. Faktisk er \(129 = 3 \cdot 43\), så 129 er altså et sammensat tal.

Vi kan lave lidt statistik over, hvor mange 1-taller der kommer, når vi opløfter alle tallene 1, 2, 3, …, m-1 til den m-1’te potens. Lad os se på de første ulige tal, større end 100:

m	101	103	105	107	109	111	113	115	117
Antal 1-taller	100	102	16	106	108	4	112	4	8

Vi ser, at enten får vi kun få 1-taller, ellers også får vi ikke andet end 1-taller (når m er et primtal).

Vi kan prøve med nogle lidt større værdier for m:

m	1001	1003	1005	1007	1009	1011	1013	1015	1017
Antal 1-taller	80	4	16	4	1008	4	1012	24	16

For m = 1001 finder vi altså 80 et-taller blandt tallene \(a^{1000}\) modulo 1001. Hvis vi derfor, for tallet m = 1001, prøver med 10 tilfældige tal, så kan vi godt ramme ind i nogle af dem der, når de opløftes i potensen 1000, giver 1 modiulo 1001. Men 80 ud af 1001 er trods alt kun 8%. Det er nogenlunde samme sandsynlighed som det at få f.eks. en 12’er med en 12-sidet terning. Det kan man godt få en gang, måske to gange i træk, men næppe 10 gange i træk.

Konklusionen er, at man kan bruge Fermats lille sætning til at undersøge om et givet tal m er et primtal. Det er ikke en vandtæt metode, man kan komme ud for at de første mange tal man prøver med alle giver et et-tal, men det er trods alt meget lidt sandsynligt.

Der findes bedre metoder, der med større sikkerhed kan afgøre om et helt tal er et primtal.

Der findes også en metode som med 100% sikkerhed kan afgøre om et helt tal er et primtal.

Python-program og grafer

Hvis m er et stort tal, så er det naturligvis ret tidskrævende, hvis man manuelt vil undersøge, hvor mange af potenserne \(a^{m-1}\) der giver 1.

Jeg har derfor lavet et lille Python-program som løser det for os.

mmax=100
 for m in range(1,mmax+1):
     antal=0
     for a in range(1,m):
         if pow(a,m-1,m)==1:
             antal+=1
     print(m,antal)

I første linie sættes mmax til 100. Derefter er der en løkke; m sættes først til 1, så til 2, så til 3, så til 4, … og til sidst til mmax.

For hver værdie af m gennemløber a en løkke, med a = 1, a = 2, a = 3, … a = m-1.

For hver værdi af m optælles så antallet af gange \(a^{m-1} \equiv 1\) modulo m. Løkken med a sætter først a til 1. Så undersøges om \(a^{m-1} \equiv 1\) modulo m. Hvis \(a^{m-1} \equiv 1\) så forøges antal med 1, eller lades antal være uændret. Herefter sættes a til 2. Så undersøges om \(a^{m-1} \equiv 1\) modulo m. Hvis \(a^{m-1} \equiv 1\) så forøges antal med 1, eller lades antal være uændret. Sådan fortsættes indtil a = m-1.

Begyndelsen af outputtet ses her:

1 0
2 1
3 2
4 1
5 4
6 1
7 6
8 1
9 2

For m = 1 er der ingen tal, som opløftet til 0’te potens, giver 1.

For m = 2 er der ét tal, som omløftet til 1’te potens, giver 1, når vi regner modulo 2.
\(0^1 \equiv 0\) og \(1^1 \equiv 1\).

For m = 3 er der to tal, som omløftet til 2’te potens, giver 1, når vi regner modulo 3.
\(0^2 \equiv 0\) , \(1^2 \equiv 1\), \(2^2 = 4 \equiv 1\).

For m = 4 er der ét tal, som omløftet til 3’te potens, giver 1, når vi regner modulo 4.
\(0^3 \equiv 0\) , \(1^3 \equiv 1\), \(2^3 = 8 \equiv 0\).

For m = 5 er der fire tal, som omløftet til 4’te potens, giver 1, når vi regner modulo 5.
\(0^4 \equiv 0\) , \(1^4 \equiv 1\), \(2^4 = 16 \equiv 1\) , \(3^4 = 81 \equiv 1\).

Jeg har så taget værdierne (outputtet), indsæt det i et regneark, og tegnet en graf:

Nedenstående figur viser sammenhængen mellem værdier af m, for m = 1, 2, 3, …, 100, og antal gange \(a^{m-1} \equiv 1\) modulo m.

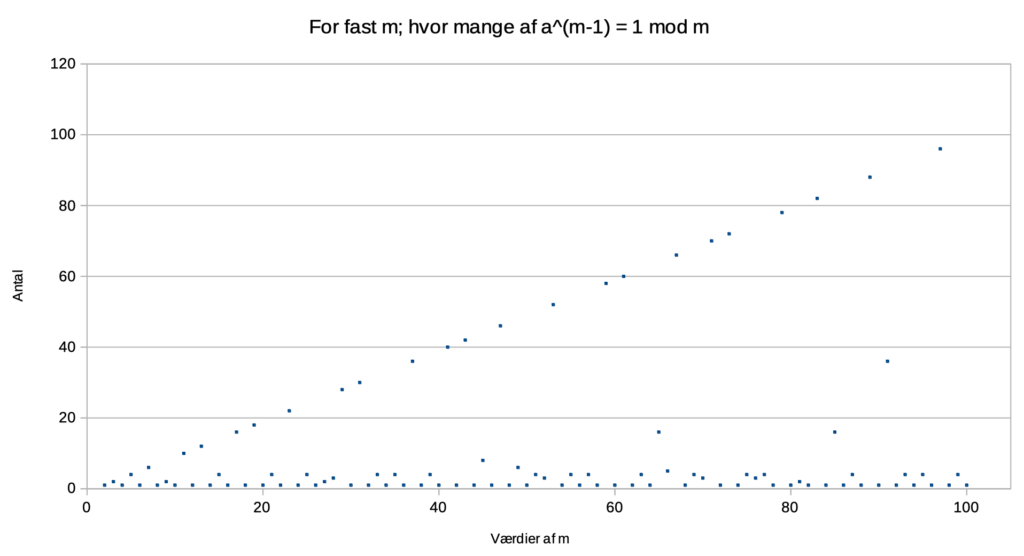
Alle prikkerne på den skrå linie kommer fra primtallene. Er m = 19, der er et primtal, så vil de 18 tal; 1, 2, 3, 4, …, 18 alle give 1, når der opløftes i potensen 19, og man regner modulo 19.

Når m således er et primtal, så vil der for alle tal a, der er mindre end m, og større end 0, gælde at \(a^{m-1} \equiv 1\) modulo m.

For m = 91, der ikke er et primtal, er der ikke mindre end 36 værdier for a, som giver 1, når de opløftes i potensen 90, når vi regner modulo 91. Det er 40% af de mulige a-værdier.

Hvis vi laver en tilsvarende figur for m = 1, 2, 3, … , 1000 får vi

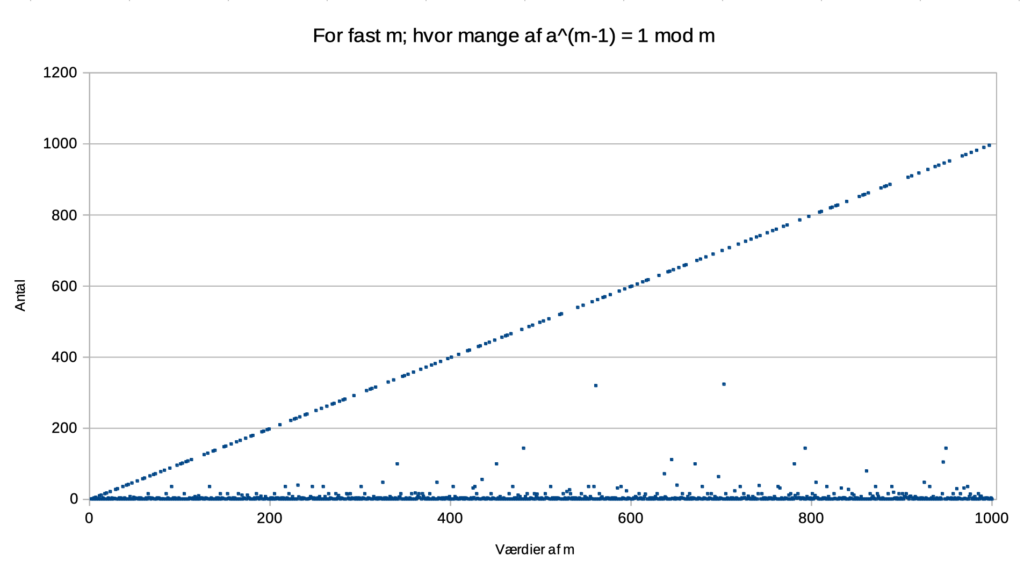
Til sidst en figur for m = 1, 2, 3, … , 10000:

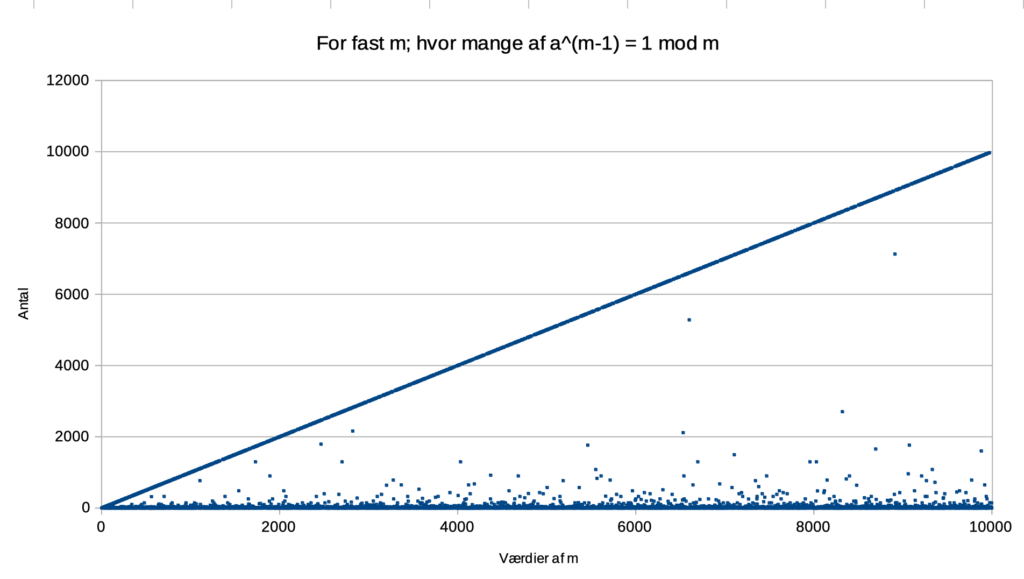
For m = 6601 er der 5280 værdier for a, som, når de opløftes i potensen 6600, giver 1, når vi regner modulo 6601. Det svarer til 80%.

For m = 8911 er der ikke mindre end 7128 værdier for a, som, når de opløftes i potensen 8910, giver 1, når vi regner modulo 8911. Det svarer også til 80%.

Antag at vi vil undersøge om tallet m er et primtal.

Vi vælger så f.eks. 10 tilfgældige tal a blandt tallene 1, 2, 3, …, m-1.

Vi undersøger, for hvert af disse, om \(a^{m-1} \equiv 1\) modulo m.

Hvis m er et primtal, så vil der for alle de 10 værdier af a gælde at \(a^{m-1} \equiv 1\) modulo m.

Hvis m ikke er et primtal, så vil der for hver af de 10 tal gælde, at sandsynligheden for, at \(a^{m-1} \equiv 1\) modulo m, normal er langt mindre end \(\frac{1}{3}\).

Sandsynligheden for, at der for alle de 10 tal gælder, at \(a^{m-1} \equiv 1\) modulo m , er dermed langt mindre end \(\left( \frac{1}{3} \right) ^{10} = 0.000017 = 0.0017\)%.

Hvis m ikke er et primtal, så er det altså ret usandsynligt at \(a^{m-1} \equiv 1\) modulo m for alle 10 forskellige værdier af a.

Lad os til sidst se på, hvor mange procent af tallene mellem 1 og m-1, for m = 1, 2, 3, …, 100000, som opfylder at \(a^{m-1} \equiv 1\) modulo m.

Jeg har optalt resultaterne, og omreget til procent. Da 0 opløftet i en potens aldrig kan give 1, så ser jeg bort fra a = 0.

Vi ved, at når m er et primtal, så vil alle a‘er, når de opløftes i potensen m-1, give 1, regnet modulo m. Så procentdelen, for alle primtal, er 100%.

Men omvendt; hvis nu procentdelen for et helt tal m er 100%, kan vi så være sikker på at m er et primtal? Dét kan der med garanti siges noget klogt om, men pointen er her, at Fermats primtalstest reelt kun kan bruges til at afvise at et tal er et primtal; får man nemlig ikke resultatet 1 når man beregner \(a^{m-1}\) mod m, for bare en værdi af a, så er m ikke et primtal

Figuren viser resultaterne:

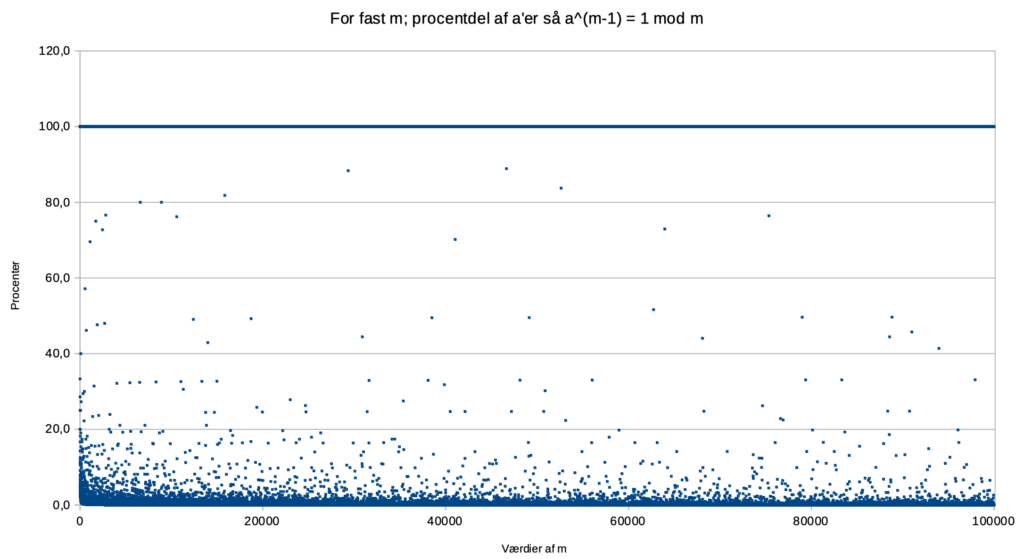
For m = 46657 vil 88.9% af a‘erne, når de opløftes i potensen 56656, give 1, når vi regner modulo 46657.

En gruppe er en mængde af elementer, og en regneoperation, som opfylder at

1 – Mængden af elementer skal være lukket mht. regneoperationen.
2 – Der skal gælde en parentesregel; a + (b + c) = (a + b) + c
3 – Der skal være et neutralt element.
4 – Alle elementer skal have et inverst element.

Vi har her brugt ‘+’ som symbol for regneoperationen. Når man bruger ‘+’ som regneoperation, så bruger man ofte ‘0’ som symbol for det neutrale element.

Lad os se på \(\mathbb{Z}_n\) når \(n=10\).

Vi vil altså her se på \(\mathbb{Z}_{10}\).

Denne mængde består af de 10 elementer

\(0, 1, 2, 3, 4, 5, 6, 7, 8, 9\)

Den tilhørende regneopeartion er ‘+’. Man adderer altså to elementer, ved at lægge dem sammen som man plejer. Får man en sum som er større end 9, så ‘reguleres ned’ modulo 10:

\(2+2 = 4 \equiv_{10} 4\)
\(4+4 = 8 \equiv_{10} 8\)
\(8+8=16 \equiv_{10} 6 \)

Det er let at lave en additionstabel:

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	0
2	2	3	4	5	6	7	8	9	0	1
3	3	4	5	6	7	8	9	0	1	2
4	4	5	6	7	8	9	0	1	2	3
5	5	6	7	8	9	0	1	2	3	4
6	6	7	8	9	0	1	2	3	4	5
7	7	8	9	0	1	2	3	4	5	6
8	8	9	0	1	2	3	4	5	6	7
9	9	0	1	2	3	4	5	6	7	8

Jeg har farvet tallet 2 i første kolonne og tallet 3 i første række røde. Disse to tal, lagt sammen, giver 5. Derfor er 5-tallet inde i tabellen også farvet rødt.

Jeg har farvet tallet 6 i første kolonne og tallet 7 i første række blå. Disse to tal, lagt sammen, giver 13. 13 er kongruent med 3 modulo 10. Derfor er 3 tallet inde i tabellen farvet blåt.

Mængde \(\mathbb{Z}_{10}\) med regneoperationen ‘+’ udgør en gruppe. Tallet ‘0’ er det neutrale element.

Betingelsen ‘1 – Mængden af elementer skal være lukket mht. regneoperationen’ er opfyldt, for når vi adderer to tal, og reducerer modulo 10, så får vi igen et element i \(\mathbb{Z}_{10}\).

Betingelsen ‘2 – Der skal gælde en parentesregel; a + (b + c) = (a + b) + c‘ er opfyldt, for parentesreglen gælder for de almindelige tal, så ventres side bliver altis lig højre side, og når vi reducerer modulo n så får vi altså samme resultat.

Betingelsen ‘3 – Der skal være et neutralt element’ er opfyldt; tallet ‘0’ er nelig et neutralt element, for lægges det til ethvert element i \(\mathbb{Z}_{10}\) får vi uændret samme element. Det ses også af tabellen, hvor række 2, med 0 til ventre, bare består af tallene 0, 1, 2, …, 9. Vi ser også at 2. søjle, søjlen med et 0 for oven, også består af tallene 0, 1, 2, …, 9.

Betingelsen ‘4 – Alle elementer skal have et inverst element’ er opfyldt. F.eks. har 7 et inverst element. Lægger man nemlig 3 til 7, så får man 10, der er kongruent med 0 modul 10. Elementet 3 er altså det inverse element til elementer 7. Hvis man ser ned gennem tabellen, så ser man at der er 0’er i alle rækker. Alle elementer i \(\mathbb{Z}_{10}\) har dermed et inverst element.

Nu tænker du nok; Gad vide hvad en gruppe er. Og hvad kan det med grupper bruges til?

Måske tænker du? Skal jeg ikke bare springe det med grupper over, det virker list mystisk, det er nok for svært for mig. Men brug nu 15 minutter på at læse testen, tænk over hvad der står, og så har du styr på hvad en gruppe er.

Det med grupper er egentlig ikke så svært. Det er måske lidt abstrakt, men det er ikke svært. Hvis man arbejder med matematik, så lægger man måske mærke til, at man, i en masse forskellige tilfælde, står over for de samme problemer/udfordringer. Måske lægger man mærke til, at de ting man arbejder med, opfører sig på sammen måde, og at de opgaver man skal løse, kan løses på samme måde, selv om der er tale om helt forskellige ting. Her skal læseren se en masse konkrete eksempler/opgaver for sig, som måske, i første omgang, ikke har noget med hinanden at gøre, men som faktisk kan løses på præcis samme måde. At de kan løses på præcis sammen måde skyldes måske, at det er samme slags problemer, bare i forskellige forklædninger. Matematikeren ser måske dette, og laver så en generel teori der beskriver de forskellige konkrete eksempler, og forklarer hvordan opgaver kan løses. Gruppeteori er noget abstrakt matematik, som kan bruges i en masse konkrete tilfælde.

Måske har jeg hægtet læseren af her, for hvad mener jeg? Hvis du går i gymnasier, så kender du til lineær vækst. Det er noget med y = ax + b. Lineær vækst kan bruges til at beskrive en masse konkrete eksempler. Selve teorien om lineær vækst er en abstrakt teori, der ikke er bundet til eksemplerne. Teorien for lineær vækst kommer fra, at en matematiker, en gang for længe siden, har set en masse fællestræk ved en masse konkrete opgaver. Matematikeren har så lavet en abstraktv teori om ‘ineær vækst’. Den generelle teori om lineær vækst kan så bruges i en masse konkrete eksempler; taletidskort, taxakørsel, …

Eller et mere jordnært eksempel: Når man tager kørekort, så lærer man at køre bil. Man lærer ikke at køre Volvo. Man lærer ikke at køre Opel. Man lærer at køre i den abstrakte størrelse der kaldes for’ bil’. Grunden til at det giver mening, altså det at lære at køre bil, er, at alle biler, mere eller mindre, opfører sig på samme måde. Der er et rat, der er et gear, der er nogle pedaler m.v. Når man har lært at køre ‘bil’, så kan man køre Volvo, så kan man køre Opel, …

Når man har taget kørekort til ‘grupper’, så ved man hvordan man arbejder med grupper, og man ved hvilke regler der gælder for grupper. Når man så møder en konkret gruppe, så kan den generelle teori, som man har lært, bruges til det konkrete tilfælde.

Nok snak. Tilbage til det med grupper.

Vi ved alle hvad der menes med en gruppe mennesker. Men hvad menes der med en gruppe, i matematik?

I matematik er en gruppe ikke anden end en mængde af elementer, og en regneoperation, som opfylder de fire krav:

1 – Mængden af elementer skal være lukket mht. regneoperationen.
2 – Der skal gælde en parentesregel; a + (b + c) = (a + b) + c
3 – Der skal være et neutralt element.
4 – Alle elementer skal have et inverst element.

Lad og sige at vores regneoperation er ‘+’.
Kalder vi elementerne for a, b, c, … så kan de fire krav, til det at være en grupper, skrives

1 – Summen a + b af to elementer a og b skal også være et element i mængden af elementer.
2 – Der skal gælde at a + (b + c) = (a + b) + c.
3 – Der skal være et nul-element 0 (nul).
4 – For hvert element a skal der findes et andet element b, således at a + b = 0 (og b + a = 0).

I nogle grupper er a + b ikke lig b + a, så derfor står der i punkt 4 at der både skal gælde at a + b = 0 og b + a = 0.

Som huskeregel for de krav, der er til det at være en gruppe, kan man bruge ‘CAN I’.

Bogstavet ‘C’ står for ‘Closed’, dvs. lukket. Bogstavet ‘A’ så for ‘Associativ’, som er navnet på parentesreglen. Bogstavet ‘N’ så for ‘Neutralt element’. Bogstavet ‘I’ står for ‘Inverst element’.

Det lyder måske lidt mystisk, og for folk der er vant til at bruge ‘grupper’ er det nok trivielt, men for os andre er det med grupper en noget mystisk ting, som ikke siger de fleste ret meget. Men prøv at huske på ‘CAN I’, og se se på eksemplerne herunder.

C = Closed = Lukket
A = Associativ regel: a + (b + c) = (a + b) + c
N = Neutral element N
I = Alle elementer har et inverst element, summen af de to lig N.

Eksempel 1

Lad og se på mængden af de hele tal. Som regneoperation tager vi ‘plus’, dvs. ‘+’.

Påstanden er nu, at mængden af hele tal, med regneoperationen ‘plus’, er en gruppe.

1 – Lægger vi to hele tal sammen, så får vi et nyt helt tal. Mængden af hele tal, sammen med ‘plus’, er altså lukket.
2 – For hele tal gælder at a + (b + c) = (a + b) + c. F.eks. er 6 + (4 + 3) = (6 + 4) + 3. Det er derfor man ikke skriver parenteser når man skriver 6 + 4 + 3, for det er lige meget i hvilken rækkefølge man lægger tallene sammen. Hvis rækkefølgen betød noget, så skulle man nemlig indsætte parenteser.
3 – Det neutrale element er 0. Når man lægger tallet 0 til et helt tal a, så gælder jo at a + 0 = a og 0 + a = a .
4 – Alle elementer skal have et inverst element. Elementet 7 har f.eks. det inverse element -7. Det skyldes at 7 + (-7) = 7 – 7 = 0.

Eksempel 2

Lad os nu prøve selv at lave en gruppe. Vi siger at der skal være fire elementer i grupper. Lad os kalde de fire elementer for a, b, c og d.

I sidste afsnit så vi på kongruens. Nu skal vi se lidt på restklasser. De to begreber kongruens og restklasser hænger sammen.

Vi ser først på kongruens modulo 5. Vi skriver tallene 0, 1, 2, 3, 4 i første række i en tabel.

0	1	2	3	4
5	6	7	8	9
10	11	12	13	14
15	16	17	18	19
20	21	22	23	24
25	26	27	28	29
30	31	32	33	34
35	36	37	38	39
40	41	42	43	44
45	46	47	48	49

Når vi skriver at \(2+3=5\), så er lighedstegnet et tegn der fortæller, at summen af tallene 2 og 3 er det samme som tallet 5. Lighedstegnet fortæller altså, at tallet på venstre side er lige så stort som tallet på højre side.

Når vi skriver \(17 \equiv 42\) så står der også hele tal på begge sider. Tallene på de to sider er ikke ens, men de står i den samme søjle i tabellen. På samme måde er \(2+3 \equiv 0\). På venstre sider står der tallet 5, skrevet som en almindelig sum af tallene 2 og 3. Men 5 ligger jo i samme søjle som tallet 0. Derfor er \(2+3 \equiv 0\).

Under tallet 0 i første række står der tallene 5, 10, 15, 20, 25, … Alle disse tal er naturligvis ikke lig med tallet 0. F.eks. er 5 jo ikke lig med 10. Men tallene 5, 10, 15, 20, 25, … er alle kongruente med tallet 0.

\(5 \equiv 0 \:,\: 10 \equiv 0 \:,\: 15 \equiv 0 \:,\: 20 \equiv 0 \:,\: ...  \)

Det er klart, at alle hele tal er kongruente med ét af tallene 0, 1, 2, 3, 4. Tænk nemlig på et tal. Vi kan så fortsætte tabellen øverst i det uendelige, og på et eller andet tidspunkt så vil vi nå frem til det tal du tænker på. Øverst i den søjle hvor dette tal står, finder vi et af tallene 0, 1, 2, 3, 4. Det tal, du tænkte på, er så kongruent med tallet i første række, lodret over dit tal.

Negative tal, som -117, er også kongruent med et af tallene 0, 1, 2, 3, 4. Tabellen skal bare fortsættes i negativ retning, og på et eller andet tidspunkt støder vi på tallet -117.

Et tal som 2177 er også kongruent med ét af tallene 0, 1, 2, 3, 4. Men hvilket? Hvis vi ikke vil udfylde tabellen indtil vi når tallet 2177, hvad gør vi så? Lad os se på en del af tabellen fra før:

0	1	2	3	4
5	6	7	8	9
10	11	12	13	14
15	16	17	18	19

Vi kan skrive alle tal der er større end 4 på en anden måde:

0	1	2	3	4
\(1 \cdot 5 + 0\)	\(1 \cdot 5 + 1\)	\(1 \cdot 5 + 2\)	\(1 \cdot 5 + 3\)	\(1 \cdot 5 + 4\)
\(2 \cdot 5 + 0\)	\(2 \cdot 5 + 1\)	\(2 \cdot 5 + 2\)	\(2 \cdot 5 + 3\)	\(2 \cdot 5 + 4\)
\(3 \cdot 5 + 0\)	\(3 \cdot 5 + 1\)	\(3 \cdot 5 + 2\)	\(3 \cdot 5 + 3\)	\(3 \cdot 5 + 4\)

Vi lægger mærke til, at

– alle tal i kolonnen med et 0 øverst kan skrives som et helt tal gange 5.
– alle tal i kolonnen med et 1-tal øverst kan skrives som et helt tal gange 5, plus 1.
– alle tal i kolonnen med et 2-tal øverst kan skrives som et helt tal gange 5, plus 2.
– alle tal i kolonnen med et 3-tal øverst kan skrives som et helt tal gange 5, plus 3.
– alle tal i kolonnen med et 4-tal øverst kan skrives som et helt tal gange 5, plus 4.

Den opmærksomme læser vil måske genkende regnestykkerne i tabellen herover som noget der kommer fra heltalsdivision.

Hvis vi dividerer f.eks. 17 med 5, så går divisionen ikke op, der kommer en rest på 2:

\(17 = 3 \cdot 5 + 2 \)

Det kan illustreres således:

Dermed ser vi at

– alle tal i kolonnen med et 0 øverst giver en rest på 0 ved division med 5.
– alle tal i kolonnen med et 1 øverst giver en rest på 1 ved division med 5.
– alle tal i kolonnen med et 2 øverst giver en rest på 2 ved division med 5.
– alle tal i kolonnen med et 3 øverst giver en rest på 3 ved division med 5.
– alle tal i kolonnen med et 4 øverst giver en rest på 4 ved division med 5.

Her findes forklaringen på begrebet restklasser. Tager man et helt tal, og dividerer det med 5, så får man en rest på 0, 1, 2, 3 eller 4. Resten (ved divisionen) fortæller altså hvilket af tallene 0, 1, 2, 3, 4 som tallet er kongruent med.

Restklassen 0 er de hele tal, så er kongruente med 0. Restklassen 1 er de hele tal, som er kongruente med 1. Restklassen 2 er de hele tal, som er kongruente med 2. Restklassen 3 er de hele tal, som er kongruente med 3. Restklassen 4 er de hele tal, som er kongruente med 4.

En restklasse er altså ikke et tal, men en samling af uendelige mange tal:

\(\bold{0} \;=\; \{... \;,\; -15 \;,\; -10 \;,\; -5 \;,\; 0 \;,\; 5 \;,\; 10 \;,\; 15 \;,\; ...\}\)

\(\bold{1} \;=\; \{... \;,\; -14 \;,\; -9 \;,\; -4 \;,\; 1 \;,\; 6 \;,\; 11 \;,\; 16 \;,\; ...\}\)

\(\bold{2} \;=\; \{... \;,\; -13 \;,\; -8 \;,\; -3 \;,\; 2 \;,\; 7 \;,\; 12 \;,\; 17 \;,\; ...\}\)

\(\bold{3} \;=\; \{... \;,\; -12 \;,\; -7 \;,\; -2 \;,\; 3 \;,\; 8 \;,\; 13 \;,\; 18 \;,\; ...\}\)

\(\bold{4} \;=\; \{... \;,\; -11 \;,\; -6 \;,\; -1 \;,\; 4 \;,\; 9 \;,\; 14 \;,\; 19 \;,\; ...\}\)

Eksempel 1

Lad os finde ud af hvilken restklasse talet 4321 hører til.

Vi dividerer 4321 med 5. Tallet 5 går 864 gange op i 4321, og der er en rest på 1:

\(4321 = 864 \cdot 5 + 1\)

Dermed er \(4321 \equiv 1\), og tallet 4321 hører til restklassen 1.

Eksempel 2

Lad os nu se på kongruens modulo 18.

Antag at vi skal finde du af hvilket af tallene 0, 1, 2, 3, 4, … , 17 som tallet 654321 er kongruent med.

Det er ikke indlysende hvad svaret er. Men lad os dividere 654321 med 18:

\(\frac{654321}{18}=36351.1666667\)

Resultatet fortæller, at 654321 kan skrives som 36351 18’ere, og en rest. Da \(36351 \cdot 18 = 654318\), så mangler vi 3 for at komme helt op til 654321. Vi har altså at

\(654321 = 36351 \cdot 18 + 3\)

Ved divisionen får man en rest på 3, og dermed er 654321 kongruent med 3.

Tallet 654321 hører dermed til restklassen 3 når vi ser på kongruens modulo 18.

Under udarbejdelse….læs ikke videre 🙂

Når man skriver \(\bbbZ_n\), så mener man elementerne 0, 1, 2, 3, 4, … n. Elementerne i \(\bbbz_n\) kan kombineres med addition; ‘+’. Man kan altså lægge elementer sammen i \(\bbbz_n\). Når man har lagt to elementer sammen, så får man et nyt element i

Når man skriver \((\bbbz_n)^*\), så mener man de elementer blandt 0, 1, 2, 3, 4, …, som er primiske med n. Elementerne i \((\bbbz_n)^*\) kan kombineres med multiplikation ‘\(\cdot\)‘. Man kan altså lægge elementer sammen i \((\bbbz_n)^*\),

Vi vi i dette afsnit se på mængden \((\mathbb{Z}_5)^*\), der indeholder de fem elementer 0, 1, 2, 3, 4.

Vi skal se på hvordan man multiplicerer to elementer, dvs. hvordan man ganger to elemeter fra \(\mathbb{Z}_5\) med hinanden. Vi bruger symbolet ‘\(\cdot\)‘ for gange.

Vores legeplads i dette afsnit er altså de fem elementer \({ \:0, \:1 , \:2, \:3, \:4 }\), og vi skal se på regler for hvordan man lægger to elementer sammen og hvordan man ganger to elementer.

Det, at vi har valgt at kalde de fem elemener i \(\mathbb{Z}_5\) for 0, 1, 2, 3, 4 er forpligtende. Skal man addere 1 og 2, så skulle man gerne få 3. Sådan er det med de helt tal. Det vil være forvirrende hvis 1 + 2 = 4.

Vi går lige til sagen. Vi laver en tabel for addition og en tabel for multiplikation:

+	0	1	2	3	4
0	0	1	2	3	4
1	1	2	3	4	0
2	2	3	4	0	1
3	3	4	0	1	2
4	4	0	1	2	3

\(\cdot\)	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4	1	3
3	0	3	1	4	2
4	0	4	3	2	1

Den måde tabellerne udfyldes på, er ved at se på det talskema vi har set tidligere:

0	1	2	3	4
5	6	7	8	9
10	11	12	13	14
15	16	17	18	19
20	21	22	23	24

Som almindelige hele tal har vi f.eks. at 2 + 3 = 5. Men 5 er kongruent med 0, så i vores mængde \(\mathbb{Z}_5\) er \(2 + 3 =5 \equiv 0 \), og der ser man i additionstabellen.

På samme måde så vil der for de helt almindelige hele tal gælde, at \(4 \cdot 4 = 16\). Men da 16 er kongruent med 1, så gælder i \(\mathbb{Z}_5\) at \(4 \cdot 4 = 16 \equiv 0\). Det ser vi også i multiplikations-tabellen.

For at lave regneregnerne for de fem elementer i \(\mathbb{Z}_5\), så går vi altså nogle gange ‘ud’ af mængden \(\{ \:0, \:1 , \:2, \:3, \:4 \}\) , men med kongruens fører vi resultatet tilbage igen til mængden \(\{ \:0, \:1 , \:2, \:3, \:4 \}\).

Dette afsnit hedder restklasser, og det er præcis det mængen \(\mathbb{Z}_5\) bestående af 5 elemener er, med de regneregler der er defineret i de to tabelle.

Det er desuden klart hvad \(\mathbb{Z}_5\) er, og det burde være klart hvordan vi regner i \(\mathbb{Z}_5\).

I dette afsnit skal vi se på division med heltal.

Lad os sige at vi skal lægge nogle brædder i forlængelse af hinanden, så de samlet har en længde på 20 meter. Måske skal vi lave et stakit der skal være 20 m langt.

I byggemarkedet har de brædder der er 3 m lange. Hvor mange af dem skal vi bruge, for at vi kan sætte dem i forlængelse af hinanden, og nå op på 20 m?

Figuren viser at vi skal bruge 6 hele brædder med en længde på 3 m, og så er der en rest på 2 m. Vi må naturligvis købe 7 brædder, eller har vi ikke nok.

Hvis vi vil beregne hvor mange brædder vi skal købe, så skal vi dividere 20 med 3. Vi skal nemlig finde ud af hvor mange gange 3 går op i 20. Da 20 ikke er i 3-tabellen, så går divisionen ikke op; der komme en rest. Divisionen kan skrives som

\(20 = 6 \cdot 3 + 2\)

Man kalder tallet 20 for dividenden. Tallet 3 er divisoren. Når man har udført divisionen, altså bestemt tallene 6 og 2, så kalder man 6 for kvotienten og man kalder 2 for resten.

Mere generelt:

• Det tal, der skal deles, kaldes for dividenden.
• Det tal, vi deler med, kaldes for divisoren.
• Det hele antal gange divisoren går op i dividenden kaldes for kvotienten
• Det, der er til overs ved divisonen, kaldes for resten.

Man kan altså skirve en division som

\(\textrm{dividend} = \textrm{kvotient} \cdot \textrm{divisor} + \textrm{rest}\) 

Eksempel

Vi vil dividere 19 med 5. Vi ser at 5 går op 3 gange i 19, med en rest.

Resten er \(19 – 5 \cdot 3 = 19-15 = 4\).

Dermed har vi at

\(19 = 3 \cdot  5  + 4\)

Dividenden er altså tallet 19. Divisoren er tallet 5. Kvotienten er tallet 3. Resten er tallet 4.

Antag at vi har to hele tal a og b. Vi vil finde det største hele tal, som både går op i tallet a og i tallet b. Dette tal kaldes for den største fælles divisor.

Den største fælles divisor for to hele tal a og b skrives som sfd(a, b). På engelsk skriver man gcd(a, b).

Eksempler:

Lad os se på de to tal a = 2 og b = 4.
De eneste tal der går op i 2 er tallene 1 og 2. 
De eneste tal der går op i 4 er tallene 1, 2 og 4. 
Dermed er sfd(2, 4) = 2.

Lad os se på de to tal a = 2 og b = 6.
De eneste tal der går op i 2 er tallene 1 og 2. 
De eneste tal der går op i 6 er tallene 1, 2 og 3. 
Dermed er sfd(2, 6) = 2.

Lad os se på de to tal a = 4 og b = 6.
De eneste tal der går op i 4 er tallene 1, 2 og 4. 
De eneste tal der går op i 6 er tallene 1, 2 og 3. 
Dermed er sfd(4, 6) = 2.

Lad os se på de to tal a = 12 og b = 9.
De eneste tal der går op i 12 er tallene 1, 2, 3, 4, 6, 12. 
De eneste tal der går op i 9 er tallene 1, 3 og 9. 
Dermed er sfd(12, 9) = 3.

Lad os se på de to tal a = 12345 og b = 2345.

De eneste tal der går op i 12345 er tallene 
1, 3, 5, 15, 823, 2469, 4115, 12345.

De eneste tal der går op i 2345 er tallene 
1, 5, 7, 35, 67, 335, 469, 2345.

Dermed er sfd(12345, 2345) = 5.

Når tallene a og b er store tal, så kan man ikke sådan lige finde de tal der går op i hver af dem.

Det er her Euklids algoritme kommer ind i billedet. Euklids algoritme er en effektiv metode til at bestemme den største fælles divisor for to tal.

Euklids algoritme bruges til at bestemme den største fælles diviser for to hele tal.

Den største fælles divisor for to hele tal a og b skrives som sfd(a, b).

Euklids algoritme er en effektiv metode til at bestemme den største fælles divisor for to tal.

I Euklids algoritme udfører man den ene heltalsdivsion efter den anden.

Eksempel 1

Lad os se på et eksempel på anvendelse af Euklids algoritme.

Antag at a = 86 og b = 46. Vi vil bestemme sfd(86, 46).

Vi dividerer først 86 med 46. Vi ser, at 46 kun går én gang op i 86. Resten ved divsionen er 86-46 = 40. Dermed har vi at

\(86 = 1 \cdot \color{blue} 46 \color{black} + \color{red}40\color{black}\)

Jeg har farvet divisoren 46 blå, og jeg har farvet resten på 40 rød.

Nu skal vi dele den forrige divisor med den forrige rest. Vi skal altså dele 46 med 40. Vi ser, at 40 går præcis én gang op i 46. Resten ved divisionen er 46-40 = 6. Dermed har vi at

\(\color{blue} 46 \color{black}= 1 \cdot \color{red}40\color{black} + 6\)

Nu skal vi igen dele divisoren (her 40) med resten (her 6). Sådan fortsætter vi, indtil divisionen går op. Vi dividerer altså hele tiden divisoren med resten, indtil divisionen går op.

Alt i alt får vi, med dette eksempel:

\(86 = 1 \cdot \color{blue} 46 \color{black} + \color{red}40\color{black}\)
\(\color{blue} 46 \color{black}= 1 \cdot \color{red}40\color{black} + 6\)
\(\color{red}40\color{black} = 6 \cdot 6 + 4\)
\(6 = 1 \cdot 4 + \color{red}2\color{black}\)
\(4 = 2 \cdot 2 + 0\)

Til sidst går divisionen op. Den sidste rest, der ikke er lig nul, er så den største fælles divisor. I dette tilfælde er det tallet 2, som jeg har farvet rødt.

Dermed er sfd(86, 46) = 2.

Eksempel 2

Et andet eksempel. Vi vil bestemme sfd(124, 56).

\(124 = 2 \cdot \color{blue} 56 \color{black} + \color{red}12\color{black}\)
\(\color{blue} 56 \color{black}= 4 \cdot \color{red}12\color{black} + 8\)
\(\color{red}12\color{black} = 1 \cdot 8 + \color{red}4\color{black}\)
\(8 = 2 \cdot 4 + 0\)

Dermed er sfd(124, 56) = 4.

Hvorfor virker Euklids algoritme?

Antag at vi vil bestemme sfd(a, b).

Vi skal altså bestemme det største hele tal som både går op i a og i b.

Vi dividerer a med b, og får en rest r:

\(a = q \cdot b + r\)

På figuren herunder er tegnet et liniestykke med længden a og et liniestykke med længden b.

Det røde tynde rektangel skal forestille en målestok.

Antag at a er lige så lang som et helt antal målestokke, og at b er lige så lang som et helt antal målestokke. Da må resten r også være lige så lang som et helt antal målestokke.

Og omvendt, er b er lige så lang som et helt antal målestokke, og er resten r lige så lang som et helt antal målestokke, så må a være lige så lang som et helt antal målestokke.

Sagt på en anden måde; hvis et tal går op i både a og i b, så vil tallet også gå op i resten r.

Og omvendt, hvis et tal går op i både b og i resten r, så går det også op i a.

De tal, som både går op i a og i b, er præcis de samme tal som dem der går op i b og i resten r.

Det største tal som går op i a og i b, er dermed lig det største tal som går op i b og i resten r.

Vi har altså at

\( \textrm{sfd}(a,b) = \textrm{sfd}(b,r)\)

Nu kalder jeg resten \( r \) for \(r_1\) iden næste division giver en ny rest:

\( \textrm{sfd}(a,b) = \textrm{sfd}(b,r_1) = \textrm{sfd}(r_1,r_2) = ... \)

Pythonprogram

Herunder er vist et lille Pythonprogram som udfører Euklids algoritme.

Først indtaster man de to tal a og b.

I funktionen sfd(a, b) printes mellemregninger på formen

\(\textrm{dividend} = \textrm{kvotient} \cdot \textrm{divisor} + \textrm{rest}\)

Tallet a er dividenden. Kvotienten beregnes ved brug af a // b der beregner hvor mange hele gange b går op i a. Divisoren er tallet b. Resten, ved divisionen, beregnes ved a % b.

Funktionen sfd(a, b) returnerer divisoren og resten; det er jo de to tal der skal jo bruges til næste heltalsdivision.

While-løkken kalder funktionen sfd(a, b) så længe resten ikke er lig nul.

a = int( input('Indtast et helt tal ') )
b = int( input('Indtast et helt tal ') )

def sfd(p,q):
    print(a ,"=",a//b,"*",b,"+",a % b)
    return b,a % b

while True:
    a,b=sfd(a,b)
    if b==0 :
        break

Eksempel på output ved beregning af sfd(987654321, 7654321)

Indtast et helt tal 987654321
Indtast et helt tal 7654321

 987654321 = 129 * 7654321 + 246912
 7654321 = 31 * 246912 + 49
 246912 = 5039 * 49 + 1
 49 = 49 * 1 + 0

Dermed er sfd(987654321, 7654321) = 1

Eksempel på output ved beregning af sfd(6655443322, 55443322):

Indtast et helt tal 6655443322
Indtast et helt tal 55443322

 6655443322 = 120 * 55443322 + 2244682
 55443322 = 24 * 2244682 + 1570954
 2244682 = 1 * 1570954 + 673728
 1570954 = 2 * 673728 + 223498
 673728 = 3 * 223498 + 3234
 223498 = 69 * 3234 + 352
 3234 = 9 * 352 + 66
 352 = 5 * 66 + 22
 66 = 3 * 22 + 0

sfd(6655443322, 55443322) = 22.

Det skal bemærkes at Python naturligvis har en indbygget funktion som straks beregner største fælles divisor.

Et naturligt tal, der kun kan deles med tallet 1 og tallet selv, kaldes for et primtal.

Det mindste primtal er tallet 2. Tallet 1 er ikke et primtal.

De naturlige tal er mængden \(\{1, 2, 3, 4, …\}\).

Eksempler

Tallet 2 er et primtal, da det kun er deleligt med tallet 1 og tallet 2.

Tallet 3 er et primtal, da det kun er deleligt med tallet 1 og tallet 3.

Tallet 4 er ikke et primtal; det kan nemlig deles med tallene 1, 2 og 4.

Tallet 5 er et primtal, da det kun er deleligt med tallet 1 og tallet 5.

Tallet 6 er ikke et primtal; det kan nemlig deles med tallene 1, 2, 3 og 6.

Tallet 7 er et primtal, da det kun er deleligt med tallet 1 og tallet 7.

Tallet 8 er ikke et primtal; det kan nemlig deles med tallene 1, 2, 4 og 8.

Eksempel fra den virkelige verden

Antag at vi skal sætte nogle ens brædder i forlængelse af hinanden, således at den samlede længde bliver 17 meter.

I byggemarkeder har de brædder med længderne 1m, 2m, 3 m, 4 m, …, 17 m.

Hvordan kan vi sætte ens bræddert i forlængelse af hianden, således at den samlede længde bliver 17 m?

Der er faktisk kun to muligheder; enten skal vi tage 17 brædder med en længde på 1 m, eller også skal vi tage ét langt bræt med en længde på 17 m.

Forklaringen er, at 17 er et primtal, så ingen af tallene 2, 3, 4, …, 16 går op i tallet 17.

De første primtal

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 113, 127, 131, 137, 149, 151, …

Er et tal et primtal?

Det er let at afgøre om et lille tal er et primtal; det er bare at prøve efter.

Skal vi f.eks. undersøge om 251 er et primtal, så kan vi bare dividere 251 med 2, så med 3, så med 4, så med 5 o.s.v. for at se om nogle af disse tal går op i 251.

Det er klart at lige tal ikke kan gå op i 251, og man kan også let udelukke en del andre tal på vejen som man ikke behøver at dividere op i 251. Hvis f.eks. 3 ikke går op i 251, så går 9 heller ikke op i 251. Hvis 9 nemlig går op i 251, så vil 3 gå to gange op i 251.

Desuden behøver man ikke dividere med alle tal, helt op til 251, for at undersøge om 251 er et primtal. Det er nok at prøve med tallene op til 15.

Det skyldes, at \(\sqrt{251}=15.84\). Dermed er \(251 = 15.84 \cdot 15.84\). Hvis 251 kan skrives som \( a \cdot b\), hvor a og b er heltal, med f.eks. a større end 15,84, så må b være mindre end 15,84.

Har vi derfor prøvet at dividere 251 med alle hele tal op til 15, uden at andre end tallet 1 går op, så kan ingen andre tal gå op i 251. Hvis et tal over 15 gik op i 251, så ville der jo også være et tal under 15 som går op i 251.

Hvis man vil undersøge om meget store tal er primtal, så kan man ikke bare afprøve alle muligheder. Det kan jo ikke nytte noget at det tager 1 mio år, på den hurtigste computer, at undersøge om et tal er et primtal. Der er flere andre, og smarte metoder, som på kort tid kan afgøre om et tal er et primtal.

RSA-kryptering bygger på, at tager man to meget store primtal \(p\) og \(q\), og ganger dem med hinanden; \(n = p \cdot q\), så kan man ikke på nogen let måde bestemme \(p\) eller \(q\) alene ud fra tallet \(n\). Det er altså let at gå den ene vej; det med at gange de to primtal, men det er meget vanskeligt at gå den anden vej; det med, ud fra kendskab til n, at finde p eller q.

Bemærk at det er ret let at afgøre om tallet n er et primtal; det er det naturligvis ikke da både p og q går op i det. Men det hjælper ikke på opgaven med at bestemme p eller q.

Aritmetikkens fundamentalsætning

Primtal spille en stor rolle i talteorien. En vigtig sætning er aritmetikkens fundamentalsætning. Den fortæller, list løst, at alle hele tal er bygget op af primtal.

Det vises lettest med nogle eksempler:

\(2 = 2\)
\(3 = 3\)
\(4 = 2 \cdot 2 = 2^2\)
\(5 = 5\)
\(6 = 2 \cdot 3\)
\(7 = 7\)
\(8 = 2 \cdot 2 \cdot 2 = 2^3\)
\(9 = 3 \cdot 3 = 3^2\)
\(10 = 2 \cdot 5\)
\(11 = 11\)
\(12 = 2 \cdot 2 \cdot 3 = 2^2 \cdot 2\)
\(13 = 13\)
\(14 = 2 \cdot 7\)
\(15 = 3 \cdot 5\)

På venstre side har jeg tallene 2, 3, 4, … og på højre side står der, hvordan disse tal er opbygget af primtal.

Aritmetikkens fundamentalsætning siger, at alle tal kan skrives som et produkt af primtal, dvs. som primtal ganget med hinanden. Sætningen siger også at det kun kan gøres på én måde. Her er det underforstået, at det at bytte om på to tal, ikke tæller som anden måde; \(6 = 2 \cdot 3\) og \(6 = 3 \cdot 2\) er altså ikke to forskellige måder.

Når man har skrevet et helt tal som et produkt af primtal, så siger man, at man har lavet en primfaktoropløsning af tallet.

Vi kan vælge lidt større eksempler:

\(100 = 2^2 \cdot 5^2\)
\(12345 = 3 \cdot 5 \cdot 823\)
\(987654321 = 3^2 \cdot 17^2 \cdot 379721\)
\(998877665544332211 = 3^2 \cdot 11 \cdot 229 \cdot 547 \cdot 883 \cdot 9277 \cdot 9833\)

Alle de tal der står på højre side af lighedstegnet er primtal. De resultater har jeg naturligvis ikke regnet ud ved håndkraft. Jeg har brugt Maple, og funktionen ifactor( ).

I sidste afsnit så vi på Fermats lille sætning. I dette afsnit skal vi se på Eulers sætning, som er en udvidelse af Fermats lille sætning.

Fermats lille sætning siger at:

Lad p være et primtal, og lad a være et element i \(\mathbb{Z}_p\).
Er a ikke nul, så er \( a^{p-1} \equiv 1 \)

Eller mere generelt, hvor a er et vilkårligt helt tal:

Lad p være et primtal, og lad a være et vilkårligt helt tal. 
Hvis p ikke går op i a, så er \(a^{p-1} \equiv 1\)

Fermats sætning siger altså noget om potenser af a, når p er et primtal.

Men hvad nu hvis p ikke er et primtal? Hvis p ikke er et primtal, så bruger vi bogstavet n i stedet for p. Den mængde vi ser på er så mængden \(\mathbb{Z}_n\).

Hvis n = 6.

Tallet 6 er ikke et primtal, for \(6 = 2 \cdot 3\). Lad os se på potenser af a, når a ligger i \(\mathbb{Z}_{6}\):

	0	1	2	3	4	5
1	0	1	2	3	4	5
2	0	1	4	3	4	1
3	0	1	2	3	4	5
4	0	1	4	3	4	1
5	0	1	2	3	4	5

Vi ser at det kun er elementet 5 fra \(\mathbb{Z}_6\) som giver 1-taller. Bortset naturligvis fra elementet 1 som altid giver 1-taller.

Vi ser også at der kommer 1-taller når 5 opløftes til 2. potens og til 4. potens:

\(5^2 = 25 \equiv 1 \quad 5^4 = 5^2 \cdot 5^2 \equiv 1 \cdot 1 \equiv 1 \)

Hvis n = 10.

Tallet 10 er ikke et primtal, for \(10 = 2 \cdot 5\). Lad os se på potenser af a, når a ligger i \(\mathbb{Z}_{10}\):

	0	1	2	3	4	5	6	7	8	9
1	0	1	2	3	4	5	6	7	8	9
2	0	1	4	9	6	5	6	9	4	1
3	0	1	8	7	4	5	6	3	2	9
4	0	1	6	1	6	5	6	1	6	1
5	0	1	2	3	4	5	6	7	8	9
6	0	1	4	9	6	5	6	9	4	1
7	0	1	8	7	4	5	6	3	2	9
8	0	1	6	1	6	5	6	1	6	1
9	0	1	2	3	4	5	6	7	8	9

Nå ja, tænker du, fint nok, og hvad så? Vi leder, inspireret af Fermats lille sætning, efter rækker med 1-taller. Vi kan ikke finde en række der kun indeholder et enkelt 0 og så lutter 1-taller.

I rækken hvor eksponenten er 4 og i rækken hvor eksponenten er 8 er der en del 1-taller:

	0	1	2	3	4	5	6	7	8	9
4	0	1	6	1	6	5	6	1	6	1
8	0	1	6	1	6	5	6	1	6	1

Man kan passende spørge; hvorfor lige netop eksponenterne 4 og 8?

Man kan også undre sig over hvorfor det lige er elementerne 3, 5, 7 og 9 fra \(\mathbb{Z}_{10}\) som giver 1-taller.

Hvis n = 14

Lad os se på \(\mathbb{Z}_{14}\). Tallet 14 er ikke et primatal, idet \(14 = 2 \cdot 7\). Jeg har lavet tabellen med det Python-program der er vist sidst i afsnittet om Fermats lille sætning.

Vi ser igen efter rækker med mange 1-taller. Det er rækkerne med eksponenterne 6 og 12 der indeholder flest 1-taller.

	0	1	2	3	4	5	6	7	8	9	10	11	12	13
6	0	1	8	1	8	1	8	7	8	1	8	1	8	1
12	0	1	8	1	8	1	8	7	8	1	8	1	8	1

Igen kan vi spørge; hvorfor er det eksponenterne 6 og 12 som giver de mange 1-taller? Hvorfor er det lige netop elementerne 1, 3, 5, 7, 9, 11, 13 som giver 1 når de opløftes til potenserne 6 og 12?

Opsamling

Lad os lave en lille oversigt over de resultater vi fik herover:

n = 6. Elementer 1 og 5. Eksponenter 2 og 4.
n = 10. Elementer 1, 3, 7, 9. Eksponenter 4 og 8.
n = 14. Elementer 1, 3, 5, 7, 9, 11, 13. Eksponenter 6, 12.

Det er måske ikke til at se det, hvis man ikke lige ved det:

For n = 6 er tallene 1 og 5 de tal under 6, der er primiske med tallet 6.
For n = 10 er tallene 1, 3, 7, 9 de tal under 10, der er primiske med tallet 10.
For n = 14 er tallene 1, 3, 5, 7, 9, 11, 13 de tal under 14, der er primiske med tallet 14.

Måske tænker du; hvad vil det sige at to tal er primiske? To tal er primiske hvis det eneste tal, som går op i begge, er tallet 1.

Eksempler for n = 6 :
– Tallene 5 og 6 er primiske, for det eneste tal der går op i både 5 og 6 er tallet 1.
– Tallene 4 og 6 er ikke primiske, for tallet 2 går op i både 4 og 6.
– Tallene 3 og 6 er ikke primiske, for tallet 3 går op i både 3 og 6.
– Tallene 2 og 6 er ikke primiske, for tallet 2 går op i både 2 og 6.
– Tallene 1 og 6 er primiske, for det eneste tal der går op i både 1 og 6 er tallet 1.

Så fik vi styr på den ene del:

De elementer i \(\mathbb{Z}_n\), der er primiske med n, 
giver 1-taller når de opløftes til visse potenser. 

Men hvad med eksponenterne, hvordan hænger de sammen med valg af n ?

Når \(n = 6 = 2 \cdot 3\) er den mindste eksponent lig 2.
Når \(n = 10 = 2 \cdot 5\) er den mindste eksponent lig 4.
Når \(n = 14 = 2 \cdot 7\) er den mindste eksponent lig 6.

Der er tilsyneladende en sammenhæng mellem de to primtal som n er opbygget af, og den mindste eksponent som giver de mange 1-taller: Eksponenten er, i disse tre tilfælde, en mindre end det store primtal.

Find lige frem til Fermats lille sætning igen; her er eksponenten jo også \(p-1\), altså en eksponent der er en mindre end primtallet.

Det viser sig, at (den mindste) eksponent kan udregnes ved formlen

Eksponent = \((p_1-1) \cdot (p_2-1)\)

Her er \(p_1\) og \(p_2\) de to primtal som tallene n = 6, n = 10 og n = 14 er bygget op af.

Eulers sætning

Efter den lange diskussion, så er vi klar til at formulere Eulers sætning:

Lad n være et helt positivt tal, og lad a være et element i \(\mathbb{Z}_n\).
Når a er primisk med n, så er \( a^{\varphi(n)} \equiv 1 \)

Eller mere generelt, hvor n bare er et helt (positivt) tal, og a er et helt tal:

Hvis a og n er primiske, så er \(a^{\varphi(n)} \equiv 1 \)

Vi må lige slutte af med at forklare hvad \(\varphi(n)\) er; \(\varphi(n)\) er Eulers phi-funktion.

Når \( n = p_1 \cdot p_2 \), hvor \(p_1\) og \(p_2\) er to primtal, så er \(\varphi(n) = (p_1-1) \cdot (p_2-1)\) .

Eksempler:

\(\varphi(6) = (2-1) \cdot (3-1) = 1 \cdot 2 = 2\)
\(\varphi(10) = (2-1) \cdot (5-1) = 1 \cdot 4 = 4\)
\(\varphi(14) = (2-1) \cdot (7-1) = 1 \cdot 6 = 6\) 

Det var præcis de eksponenter vi fandt ved brug af tabellerne.

Opsamling

Fermats lille sætning fortæller, at \(a^{p-1} \equiv 1\) når a er primisk med primtallet p.

Eulers sætning fortæller, at \(a^{\varphi(n)} \equiv 1 \) når a er primisk med n.