Eulers sætning

I sidste afsnit så vi på Fermats lille sætning. I dette afsnit skal vi se på Eulers sætning, som er en udvidelse af Fermats lille sætning.

Fermats lille sætning siger at:

Lad p være et primtal, og lad a være et element i \(\mathbb{Z}_p\).
Er a ikke nul, så er \( a^{p-1} \equiv 1 \)

Eller mere generelt, hvor a er et vilkårligt helt tal:

Lad p være et primtal, og lad a være et vilkårligt helt tal. 
Hvis p ikke går op i a, så er \(a^{p-1} \equiv 1\)

Fermats sætning siger altså noget om potenser af a, når p er et primtal.

Men hvad nu hvis p ikke er et primtal? Hvis p ikke er et primtal, så bruger vi bogstavet n i stedet for p. Den mængde vi ser på er så mængden \(\mathbb{Z}_n\).

Hvis n = 6.

Tallet 6 er ikke et primtal, for \(6 = 2 \cdot 3\). Lad os se på potenser af a, når a ligger i \(\mathbb{Z}_{6}\):

	0	1	2	3	4	5
1	0	1	2	3	4	5
2	0	1	4	3	4	1
3	0	1	2	3	4	5
4	0	1	4	3	4	1
5	0	1	2	3	4	5

Vi ser at det kun er elementet 5 fra \(\mathbb{Z}_6\) som giver 1-taller. Bortset naturligvis fra elementet 1 som altid giver 1-taller.

Vi ser også at der kommer 1-taller når 5 opløftes til 2. potens og til 4. potens:

\(5^2 = 25 \equiv 1 \quad 5^4 = 5^2 \cdot 5^2 \equiv 1 \cdot 1 \equiv 1 \)

Hvis n = 10.

Tallet 10 er ikke et primtal, for \(10 = 2 \cdot 5\). Lad os se på potenser af a, når a ligger i \(\mathbb{Z}_{10}\):

	0	1	2	3	4	5	6	7	8	9
1	0	1	2	3	4	5	6	7	8	9
2	0	1	4	9	6	5	6	9	4	1
3	0	1	8	7	4	5	6	3	2	9
4	0	1	6	1	6	5	6	1	6	1
5	0	1	2	3	4	5	6	7	8	9
6	0	1	4	9	6	5	6	9	4	1
7	0	1	8	7	4	5	6	3	2	9
8	0	1	6	1	6	5	6	1	6	1
9	0	1	2	3	4	5	6	7	8	9

Nå ja, tænker du, fint nok, og hvad så? Vi leder, inspireret af Fermats lille sætning, efter rækker med 1-taller. Vi kan ikke finde en række der kun indeholder et enkelt 0 og så lutter 1-taller.

I rækken hvor eksponenten er 4 og i rækken hvor eksponenten er 8 er der en del 1-taller:

	0	1	2	3	4	5	6	7	8	9
4	0	1	6	1	6	5	6	1	6	1
8	0	1	6	1	6	5	6	1	6	1

Man kan passende spørge; hvorfor lige netop eksponenterne 4 og 8?

Man kan også undre sig over hvorfor det lige er elementerne 3, 5, 7 og 9 fra \(\mathbb{Z}_{10}\) som giver 1-taller.

Hvis n = 14

Lad os se på \(\mathbb{Z}_{14}\). Tallet 14 er ikke et primatal, idet \(14 = 2 \cdot 7\). Jeg har lavet tabellen med det Python-program der er vist sidst i afsnittet om Fermats lille sætning.

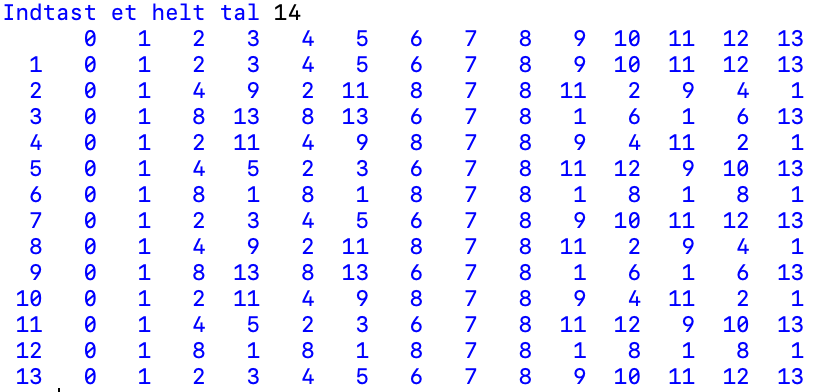
Vi ser igen efter rækker med mange 1-taller. Det er rækkerne med eksponenterne 6 og 12 der indeholder flest 1-taller.

	0	1	2	3	4	5	6	7	8	9	10	11	12	13
6	0	1	8	1	8	1	8	7	8	1	8	1	8	1
12	0	1	8	1	8	1	8	7	8	1	8	1	8	1

Igen kan vi spørge; hvorfor er det eksponenterne 6 og 12 som giver de mange 1-taller? Hvorfor er det lige netop elementerne 1, 3, 5, 7, 9, 11, 13 som giver 1 når de opløftes til potenserne 6 og 12?

Opsamling

Lad os lave en lille oversigt over de resultater vi fik herover:

n = 6. Elementer 1 og 5. Eksponenter 2 og 4.
n = 10. Elementer 1, 3, 7, 9. Eksponenter 4 og 8.
n = 14. Elementer 1, 3, 5, 7, 9, 11, 13. Eksponenter 6, 12.

Det er måske ikke til at se det, hvis man ikke lige ved det:

For n = 6 er tallene 1 og 5 de tal under 6, der er primiske med tallet 6.
For n = 10 er tallene 1, 3, 7, 9 de tal under 10, der er primiske med tallet 10.
For n = 14 er tallene 1, 3, 5, 7, 9, 11, 13 de tal under 14, der er primiske med tallet 14.

Måske tænker du; hvad vil det sige at to tal er primiske? To tal er primiske hvis det eneste tal, som går op i begge, er tallet 1.

Eksempler for n = 6 :
– Tallene 5 og 6 er primiske, for det eneste tal der går op i både 5 og 6 er tallet 1.
– Tallene 4 og 6 er ikke primiske, for tallet 2 går op i både 4 og 6.
– Tallene 3 og 6 er ikke primiske, for tallet 3 går op i både 3 og 6.
– Tallene 2 og 6 er ikke primiske, for tallet 2 går op i både 2 og 6.
– Tallene 1 og 6 er primiske, for det eneste tal der går op i både 1 og 6 er tallet 1.

Så fik vi styr på den ene del:

De elementer i \(\mathbb{Z}_n\), der er primiske med n, 
giver 1-taller når de opløftes til visse potenser. 

Men hvad med eksponenterne, hvordan hænger de sammen med valg af n ?

Når \(n = 6 = 2 \cdot 3\) er den mindste eksponent lig 2.
Når \(n = 10 = 2 \cdot 5\) er den mindste eksponent lig 4.
Når \(n = 14 = 2 \cdot 7\) er den mindste eksponent lig 6.

Der er tilsyneladende en sammenhæng mellem de to primtal som n er opbygget af, og den mindste eksponent som giver de mange 1-taller: Eksponenten er, i disse tre tilfælde, en mindre end det store primtal.

Find lige frem til Fermats lille sætning igen; her er eksponenten jo også \(p-1\), altså en eksponent der er en mindre end primtallet.

Det viser sig, at (den mindste) eksponent kan udregnes ved formlen

Eksponent = \((p_1-1) \cdot (p_2-1)\)

Her er \(p_1\) og \(p_2\) de to primtal som tallene n = 6, n = 10 og n = 14 er bygget op af.

Eulers sætning

Efter den lange diskussion, så er vi klar til at formulere Eulers sætning:

Lad n være et helt positivt tal, og lad a være et element i \(\mathbb{Z}_n\).
Når a er primisk med n, så er \( a^{\varphi(n)} \equiv 1 \)

Eller mere generelt, hvor n bare er et helt (positivt) tal, og a er et helt tal:

Hvis a og n er primiske, så er \(a^{\varphi(n)} \equiv 1 \)

Vi må lige slutte af med at forklare hvad \(\varphi(n)\) er; \(\varphi(n)\) er Eulers phi-funktion.

Når \( n = p_1 \cdot p_2 \), hvor \(p_1\) og \(p_2\) er to primtal, så er \(\varphi(n) = (p_1-1) \cdot (p_2-1)\) .

Eksempler:

\(\varphi(6) = (2-1) \cdot (3-1) = 1 \cdot 2 = 2\)
\(\varphi(10) = (2-1) \cdot (5-1) = 1 \cdot 4 = 4\)
\(\varphi(14) = (2-1) \cdot (7-1) = 1 \cdot 6 = 6\) 

Det var præcis de eksponenter vi fandt ved brug af tabellerne.

Opsamling

Fermats lille sætning fortæller, at \(a^{p-1} \equiv 1\) når a er primisk med primtallet p.

Eulers sætning fortæller, at \(a^{\varphi(n)} \equiv 1 \) når a er primisk med n.