I stedet for bare at opskrive Fermats lille sætning, som sikkert ikke siger ret mange ret meget, så lad os se på nogle eksempler.
Ideen er, som i det foregående, at få nogle mentale billeder af hvad det er Fermats sætning handler om og hvad sætningen udtaler sig om.
Når man kan se det for sig, så bliver det lettere at forstår selve sætningen, og dermed bliver det lettere at huske sætningen, og det bliver lettere at kunne anvende den, nu man ved hvad den handler om.
Lad os begynde med at se på \(\mathbb{Z}_5\):
\(\mathbb{Z}_5 = \{0, 1, 2, 3, 4 \}\)
Vi har, i et tidligere afsnit, set på hvordan man regner i \(\mathbb{Z}_5\). Regnereglerne er nedarvet fra regning med hele tal, man skal bare huske, at får man et resultat udenfor mængden \(\{0, 1, 2, 3, 4\}\), så skal man ‘føre’ det tilbage til mængden \(\mathbb{Z}_5\). Det kan man gøre ved, som tidligere, at udfylde en tabel, og så gå lodret op mod tallene 0, 1, 2, 3, 4. Eller man kan dividere resultatet med 5, og så se på ‘resten’ ved divison med 5.
Vi tager nu elementet ‘3’ fra \(\mathbb{Z}_5\). Vi udregner så potenser af dette tal:
\( 3^1 = 3 \quad 3^2=9 \equiv 4 \quad 3^3=27 \equiv 2 \quad 3^4=81 \equiv 1 \)
Det var så nogle potenser af 3.
Lad os prøve at beregner potenser af alle elementerne i \(\mathbb{Z}_5\).
Vi opskriver resultaterne i en tabel. I første række har vi de fem elementer i \(\mathbb{Z}_5\), her skrevet med fed skrift. I første søjle står eksponenterne, dvs. de tal som vi opløfter i.
| 0 | 1 | 2 | 3 | 4 | |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 1 | 4 | 4 | 1 |
| 3 | 0 | 1 | 3 | 2 | 4 |
| 4 | 0 | 1 | 1 | 1 | 1 |
Kolonnen med tallene markeret med fed grøn skrift svarer til resultatet af de beregninger vi lige udførte med potenser af 3 i \(\mathbb{Z}_5\). Det sidste tal i denne kolonne er tallet 1, der er farvet rødt.
De fire tal i tabellen, markeret med fed rød skrift, fortæller at
\( 1^4 \equiv 1 \quad 2^4 \equiv 1 \quad 3^4 \equiv 1 \quad 4^4 \equiv 1 \quad \)
Det ser altså ud som om at alle elementer i \(\mathbb{Z}_5\) (dog ikke tallet 0) giver 1 når det ganges med sig selv 4 gange.
For \(\mathbb{Z}_5\) har vi altså, for a = 1, a = 2, a = 3 eller a = 4, at
\(a^{5-1} \equiv 1\)
Det kunne jo være at det bare var en egenskab ved \(\mathbb{Z}_5\).
Lad os derfor se på \(\mathbb{Z}_7\), og lave en tilsvarende tabel. Vi har de 7 elementer 0, 1, 2, 3, 4, 5, 6 i første række, og eksponenterne i første søjle.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 1 | 4 | 2 | 2 | 4 | 1 |
| 3 | 0 | 1 | 1 | 6 | 1 | 6 | 6 |
| 4 | 0 | 1 | 2 | 4 | 4 | 2 | 1 |
| 5 | 0 | 1 | 4 | 5 | 2 | 3 | 6 |
| 6 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Ser vi på tallene i sidste række, der igen er skrevet med rød fed skrift, så ser vi at
\( 1^6 \equiv 1 \quad 2^6 \equiv 1 \quad 3^6 \equiv 1 \quad 4^6 \equiv 1 \quad 5^6 \equiv 1 \quad 6^6 \equiv 1 \)
Nu vil nogen måske hævne at tallene 5 og 7 er lidt specielle tal; det er nemlig primtal. Men jeg kunne have valgt alle andre primtal, så ville resultatet være det samme. Man kan så spørge hvad der vil ske hvis man ser på f.eks. \(\mathbb{Z}_{10}\), hvor tallet 10 jo ikke er et primtal da \( 10 = 2 \cdot 5\). Det ser vi ikke på her, men det kommer vi tilbage til i et senere afsnit: Eulers sætning.
I tabellen med potenserne af alle a‘er i \(\mathbb{Z}_5\) stoppede vi ved fjerde portens. Hvordan ville den næste række se ud? Det er ret let at svare på, for \(a^5 = a \cdot a^4\), så vi kommer fra række fire til række fem ved at gange med a. Da der i række fire står en masse 1’taller, så vil der i række fem står tallene 0, 1, 2, 3, 4.
| 0 | 1 | 2 | 3 | 4 | |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 1 | 4 | 4 | 1 |
| 3 | 0 | 1 | 3 | 2 | 4 |
| 4 | 0 | 1 | 1 | 1 | 1 |
| 5 | 0 | 1 | 2 | 3 | 4 |
Fermats lille sætning
Vi kan nu formulere Fermats lille sætning.
Vi ser på mængden \(\mathbb{Z}_p\), hvor p er et primtal. Når vi bruger tegnet \(\equiv\) så mener vi kongruent mht. \(\mathbb{Z}_p\), altså at vi tager et vilkårligt helt tal, og ved brug af tabellen forklaret tidligere fører det lodret op i et af tallene 0, 1, 2, 3, … , p-1. Alternativt, at vi dividerer tallet med p og ser på ‘resten’.
Lad p være et primtal, og lad a være et element i \(\mathbb{Z}_p\).
Er a ikke nul, så er \( a^{p-1} \equiv 1 \)
Mere generelt:
Lad p være et primtal, og lad a være et vilkårligt helt tal.
Hvis p ikke går op i a, så er \(a^{p-1} \equiv 1\)
Vi kan også formlere Fermats lille sætning på følgende måde:
Lad p være et primtal, og lad a være et vilkårligt helt tal. Da er \(a^p \equiv a\)
Man kan spørge om hvorfor der, i sidste version af Fermats lille sætning, ikke står noget med at p ikke må gå op i a. Forklaringen er, at hvis p ikke går op i a, så er \(a^{p-1} \equiv 1\), og ganger vi med a, så får vi at \(a^p \equiv a\). Det er det sætningen siger, så det er ok. Går p derimod op i a, så er \(a \equiv 0\), og dermed er, helt automatisk, \(a^p \equiv 0\). Så den sidste sætning gælder også hvis p går op i a, men resultatet er så ret trivielt at ‘0 = 0’.
For at slutte afsnittet af: Som billede på Fermats lille sætning, betragt den første tabel:
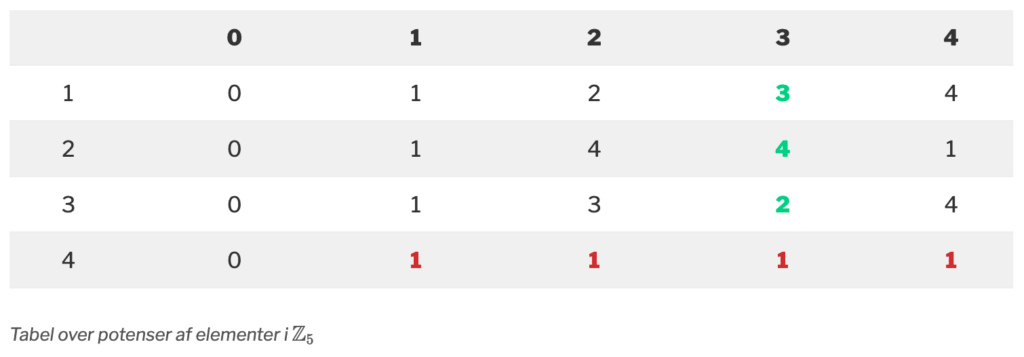
Vi ser på mængden \(\mathbb{Z}_5\). Tabellen indeholder potenser af elementerne 0, 1, 2, 3, 4 fra \(\mathbb{Z}_5\). I række 4, stå der en masse 1’taller. Det er Fermats lille sætning der siger at der skal stå 1’taller i række fire, dog ikke under 0.
Python-program
Det er, sådan set, ret trivielt at udfylde tabellerne herover med resultater. Skal man f.eks. beregne \(3^4\), så kan man gøre følgende:
\( 3^1 \equiv 3 \) \( 3^2 \equiv 3 \cdot 3 = 9 \equiv 4 \) \( 3^3 = 3 \cdot 3^2 \equiv 3 \cdot 4 = 12 \equiv 2 \) \( 3^4 = 3 \cdot 3^3 \equiv 3 \cdot 2 = 6 \equiv 1 \)
Vi går altså et skridt frem ad gangen, og reducerer hver gang så vi bliver indenfor \(\mathbb{Z}_5\). På den måde udngår vi for store tal, og vi får samme resultat som hvis vi bare beregnede \(3^4\) og så, bagefter, reducerede til \(\mathbb{Z}_5\).
Man kan også lave et lille Python-program som udfører beregningerne for en:
n = int( input('Indtast et helt tal ') )
print(" ",end=' ')
for j in range (0,n):
print(format(j, '3d'),end=' ')
print(' ')
for i in range (1,n):
print(format(i, '3d'),end=' ')
for j in range (0,n):
print(format((j**i) % n,'3d'),end=' ')
print(' ')
Jeg har ikke kommenteret programmet, men først skrives tallene 0, …, n i første række. Der indledes med nogle mellemrum så alt kommer til at stå pænt.
Så kommer der to løkker; den første, den med i, er en løkke for eksponenten, og for hver værdi af eksponenten i beregnes \(j^i\) for j = 0, 1, 2, 3, … , n-1 som skrives i samme række, så ny række, ny eksponent i, …
Eksempel på output når n = 17:

Bemærk at vi regner i \(\mathbb{Z}_{17}\) , og at der står en masse 1-taller i række 16.
