Carmichael tal – Kryptologi

Vi er ikke helt færdige med Fermats primtalstest.

I afsnittet om Fermats primtalstest diskuterer jeg hvordan man kan teste om et stort tal m er et primtal.

Mere præcist; vi så på hvor mange af tallene a = 1,2,3, …, m – 1 som opfylder at

\[a^{m-1} \equiv 1 \textrm{ mod } m \]

Hvis m er et primtal, så skal \[a^{m-1} \equiv 1 \textrm{ mod } m \] for alle værdier af a, fra a = 1, til a = m – 1.

Hvis vi bare har en værdi af a, så \[a^{m-1}\] ikke er lig 1, modulo m, så kan m ikke være et primtal.

Vi så også, at for langt de fleste tal m, som ikke er primtal, så vil de a‚er, hvor \[a^{m-1} \equiv 1 \textrm{ mod } m \], typisk kun udgøre få procent af samtlige a‚er fra a = 1 til a = m -1.

I dette afsnit vil vi ikke se på alle værdier af a, fra a = 1 til a = m – 1. Vi vil kun se på de værdier af a som er primiske med m.

Python-program

Ved at ændre minimalt i python-programmet fra forrige afsnit, så kan jeg, for hver værdi af m, optælle hvor mange af a‚erne der både er primiske med m, og som giver 1, når a opløftes i potensen m – 1. Vi regner naturligvis modulo m.

import math
mmax=1000
for m in range(1,mmax+1):
    antal=0
    antal_primiske=0
    for a in range(1,m):
        if math.gcd(a,m)==1:
            antal_primiske+=1
            if pow(a,m-1,m)==1:
                antal+=1
    print(m,antal_primiske,antal)

I pakken math, som vi importerer, ligger funktionen gcd, som beregner den største fælles divisor for to tal.

Jeg har brugt antal_primiske til at tælle de a‚er som er primiske med m.

Jeg har brugt antal til at tælle de a‚er som opfylder at \[a^{m-1} \equiv 1 \textrm{ mod } m \]. Bemærk at antal kun forøges hvis a både er primiske med m og \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Eksempel på output af første resultater:

I hver række står der tre tal;

Første tal er værdien af m.
Andet tal er antallet af a‚er, fra a = 1, til a = m -1, der er primiske med m.
Tredie tal er antallet af de tal, der er primiske med m, som også opfylder at \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Række 2: Når m = 2, så er der ét tal der er primisk med m; det er tallet 1. Og tallet 1 opfylder, at \[1^{2-1} \equiv 1 \textrm{ mod } 2 \]. Derfor står der i række 2; „2 1 1‟

\[1^{4-1} = 1^3 = 1 \equiv 1 \textrm{ mod } 4\]
\[3^{4-1} = 3^3 = 27 \equiv 3 \textrm{ mod } 4\]

Række 3: Når m = 3, så er der to tal som er primiske med m, og for begge de to tal gælder at \[a^{m-1} \equiv 1 \textrm{ mod } m \]:

\[1^{3-1} = 1^2 = 1 \equiv 1 \textrm{ mod } 3\]
\[2^{3-1} = 2^2 = 4 \equiv 1 \textrm{ mod } 3\]

Række 4. Når m = 4, så er der to tal som er primisk med m. Det er tallene 1 og 3. Opfylder de at \[a^{m-1} \equiv 1 \textrm{ mod } m \] ?

\[1^{4-1} = 1^3 = 1 \equiv 1 \textrm{ mod } 4\]
\[3^{4-1} = 3^3 = 27 \equiv 3 \textrm{ mod } 4\]

Så det er kun tallet a = 1 der både er primisk med 4 og som opfylder at \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Figur

Jeg har, for alle værdier af m fra m = 1 til m = 105, optalt antal a‚er der er primiske med m, og antal a‚er som både er primiske med m og som opfylder at \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Jag har så divideret antal med antal_primiske, og omregnet til procent.

Figuren viser resultaterne:

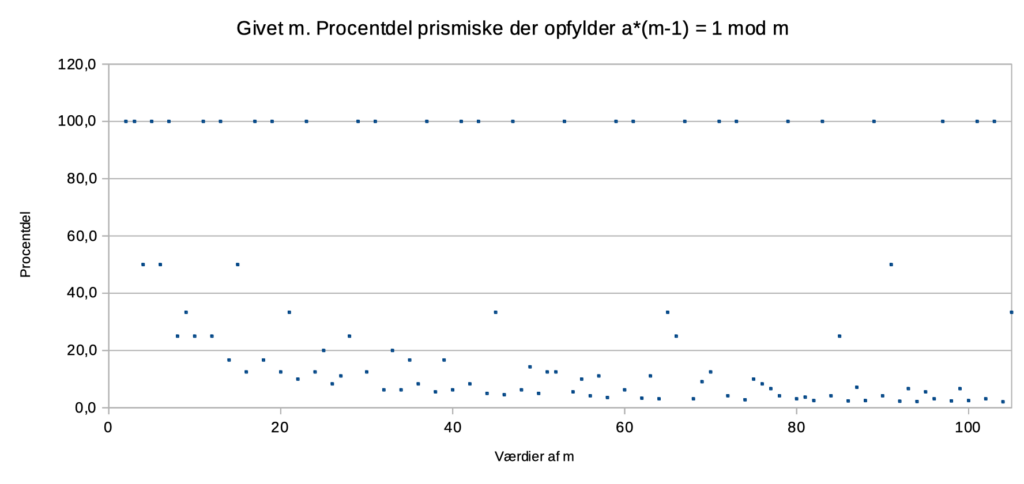
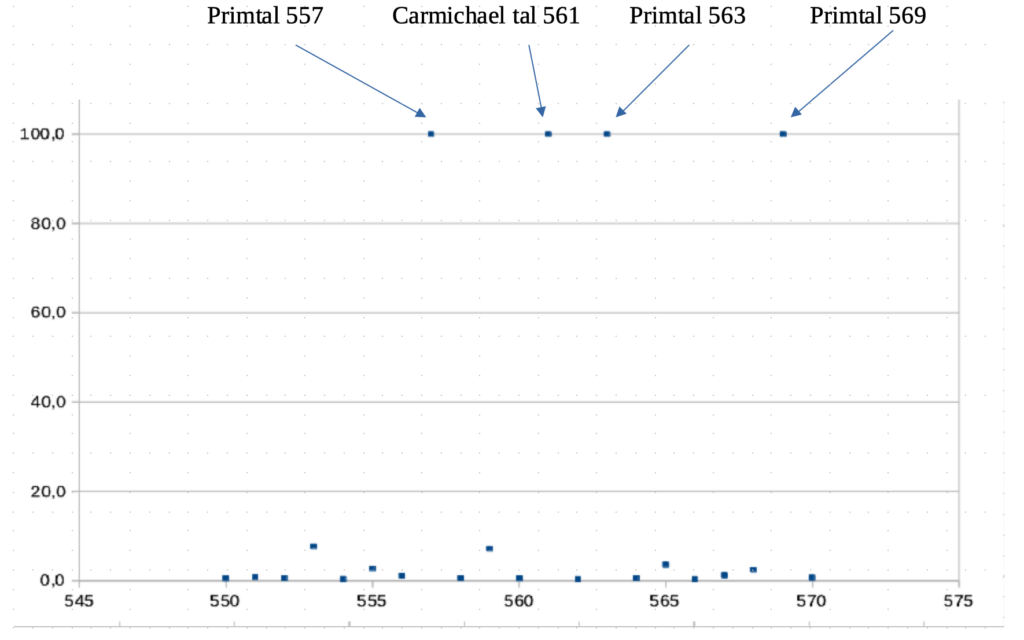
De værdier af m hvor procenten er 100 er primtallene. Når m er et primtal, så vil alle værdier af a, fra a = 1 til a = m – 1, både være primiske med m og opfylde at \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Man kan så omvendt spørge; findes der værdier af m, som ikke er primtal, hvor der for alle a‚er, som er primiske med m, også gælder at \[a^{m-1} \equiv 1 \textrm{ mod } m \] ?

Svaret er ‚ja‛, der findes sammensatte tal m som opfylder, at der for alle a‚er primiske med m, gælder at \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Disse tal kaldes Carmichael-tal. Det mindste af disse tal er 561. Der er 320 tal fra a = 1 til a = 560 som er primiske med 561. For alle disse 320 værdier af a gælder der at \[a^{560} \equiv 1 \textrm{ mod } 561 \].

Tallet 561 er ikke et primtal; \[561 = 3 \cdot 11 \cdot 17\].

Hvis vi derfor vil teste om et tal m er et primtal, og kun kontrollerer for a‚er der er primiske med m, så kan vi komme ud for værdier af m hvor alle a‚er opfylder ligningen \[a^{m-1} \equiv 1 \textrm{ mod } m \].

Figuren viser situationen.