Euklids algoritme bruges til at bestemme den største fælles diviser for to hele tal.
Den største fælles divisor for to hele tal a og b skrives som sfd(a, b).
Euklids algoritme er en effektiv metode til at bestemme den største fælles divisor for to tal.
I Euklids algoritme udfører man den ene heltalsdivsion efter den anden.
Eksempel 1
Lad os se på et eksempel på anvendelse af Euklids algoritme.
Antag at a = 86 og b = 46. Vi vil bestemme sfd(86, 46).
Vi dividerer først 86 med 46. Vi ser, at 46 kun går én gang op i 86. Resten ved divsionen er 86-46 = 40. Dermed har vi at
\[86 = 1 \cdot \color{blue} 46 \color{black} + \color{red}40\color{black}\]
Jeg har farvet divisoren 46 blå, og jeg har farvet resten på 40 rød.
Nu skal vi dele den forrige divisor med den forrige rest. Vi skal altså dele 46 med 40. Vi ser, at 40 går præcis én gang op i 46. Resten ved divisionen er 46-40 = 6. Dermed har vi at
\[\color{blue} 46 \color{black}= 1 \cdot \color{red}40\color{black} + 6\]
Nu skal vi igen dele divisoren (her 40) med resten (her 6). Sådan fortsætter vi, indtil divisionen går op. Vi dividerer altså hele tiden divisoren med resten, indtil divisionen går op.
Alt i alt får vi, med dette eksempel:
\[86 = 1 \cdot \color{blue} 46 \color{black} + \color{red}40\color{black}\]
\[\color{blue} 46 \color{black}= 1 \cdot \color{red}40\color{black} + 6\]
\[\color{red}40\color{black} = 6 \cdot 6 + 4\]
\[6 = 1 \cdot 4 + \color{red}2\color{black}\]
\[4 = 2 \cdot 2 + 0\]
Til sidst går divisionen op. Den sidste rest, der ikke er lig nul, er så den største fælles divisor. I dette tilfælde er det tallet 2, som jeg har farvet rødt.
Dermed er sfd(86, 46) = 2.
Eksempel 2
Et andet eksempel. Vi vil bestemme sfd(124, 56).
\[124 = 2 \cdot \color{blue} 56 \color{black} + \color{red}12\color{black}\]
\[\color{blue} 56 \color{black}= 4 \cdot \color{red}12\color{black} + 8\]
\[\color{red}12\color{black} = 1 \cdot 8 + \color{red}4\color{black}\]
\[8 = 2 \cdot 4 + 0\]
Dermed er sfd(124, 56) = 4.
Hvorfor virker Euklids algoritme?
Antag at vi vil bestemme sfd(a, b).
Vi skal altså bestemme det største hele tal som både går op i a og i b.
Vi dividerer a med b, og får en rest r:
\[a = q \cdot b + r\]
På figuren herunder er tegnet et liniestykke med længden a og et liniestykke med længden b.
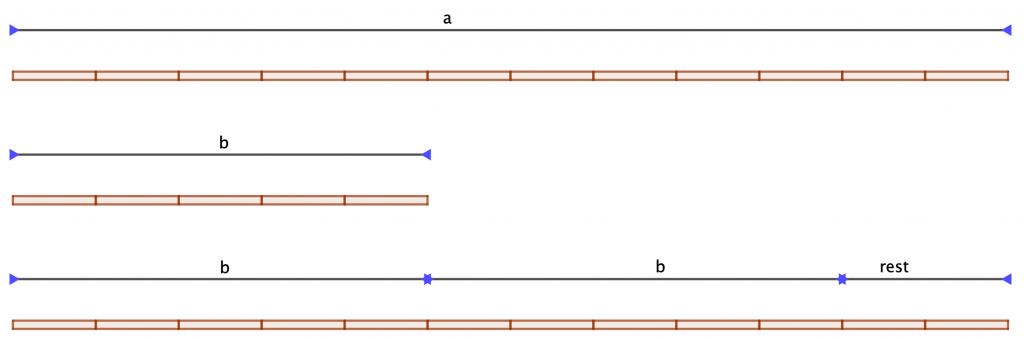
Det røde tynde rektangel skal forestille en målestok.
Antag at a er lige så lang som et helt antal målestokke, og at b er lige så lang som et helt antal målestokke. Da må resten r også være lige så lang som et helt antal målestokke.
Og omvendt, er b er lige så lang som et helt antal målestokke, og er resten r lige så lang som et helt antal målestokke, så må a være lige så lang som et helt antal målestokke.
Sagt på en anden måde; hvis et tal går op i både a og i b, så vil tallet også gå op i resten r.
Og omvendt, hvis et tal går op i både b og i resten r, så går det også op i a.
De tal, som både går op i a og i b, er præcis de samme tal som dem der går op i b og i resten r.
Det største tal som går op i a og i b, er dermed lig det største tal som går op i b og i resten r.
Vi har altså at
\[ \textrm{sfd}(a,b) = \textrm{sfd}(b,r)\]
Nu kalder jeg resten \[ r \] for \[r_1\] iden næste division giver en ny rest:
\[ \textrm{sfd}(a,b) = \textrm{sfd}(b,r_1) = \textrm{sfd}(r_1,r_2) = ... \]
Pythonprogram
Herunder er vist et lille Pythonprogram som udfører Euklids algoritme.
Først indtaster man de to tal a og b.
I funktionen sfd(a, b) printes mellemregninger på formen
\[\textrm{dividend} = \textrm{kvotient} \cdot \textrm{divisor} + \textrm{rest}\]
Tallet a er dividenden. Kvotienten beregnes ved brug af a // b der beregner hvor mange hele gange b går op i a. Divisoren er tallet b. Resten, ved divisionen, beregnes ved a % b.
Funktionen sfd(a, b) returnerer divisoren og resten; det er jo de to tal der skal jo bruges til næste heltalsdivision.
While-løkken kalder funktionen sfd(a, b) så længe resten ikke er lig nul.
a = int( input('Indtast et helt tal ') )
b = int( input('Indtast et helt tal ') )
def sfd(p,q):
print(a ,"=",a//b,"*",b,"+",a % b)
return b,a % b
while True:
a,b=sfd(a,b)
if b==0 :
breakEksempel på output ved beregning af sfd(987654321, 7654321)
Indtast et helt tal 987654321 Indtast et helt tal 7654321 987654321 = 129 * 7654321 + 246912 7654321 = 31 * 246912 + 49 246912 = 5039 * 49 + 1 49 = 49 * 1 + 0
Dermed er sfd(987654321, 7654321) = 1
Eksempel på output ved beregning af sfd(6655443322, 55443322):
Indtast et helt tal 6655443322 Indtast et helt tal 55443322 6655443322 = 120 * 55443322 + 2244682 55443322 = 24 * 2244682 + 1570954 2244682 = 1 * 1570954 + 673728 1570954 = 2 * 673728 + 223498 673728 = 3 * 223498 + 3234 223498 = 69 * 3234 + 352 3234 = 9 * 352 + 66 352 = 5 * 66 + 22 66 = 3 * 22 + 0
sfd(6655443322, 55443322) = 22.
Det skal bemærkes at Python naturligvis har en indbygget funktion som straks beregner største fælles divisor.
