I sidste afsnit så vi på kongruens. Nu skal vi se lidt på restklasser. De to begreber kongruens og restklasser hænger sammen.
Vi ser først på kongruens modulo 5. Vi skriver tallene 0, 1, 2, 3, 4 i første række i en tabel.
| 0 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 |
| 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 |
| 45 | 46 | 47 | 48 | 49 |
Når vi skriver at \[2+3=5\], så er lighedstegnet et tegn der fortæller, at summen af tallene 2 og 3 er det samme som tallet 5. Lighedstegnet fortæller altså, at tallet på venstre side er lige så stort som tallet på højre side.
Når vi skriver \[17 \equiv 42\] så står der også hele tal på begge sider. Tallene på de to sider er ikke ens, men de står i den samme søjle i tabellen. På samme måde er \[2+3 \equiv 0\]. På venstre sider står der tallet 5, skrevet som en almindelig sum af tallene 2 og 3. Men 5 ligger jo i samme søjle som tallet 0. Derfor er \[2+3 \equiv 0\].
Under tallet 0 i første række står der tallene 5, 10, 15, 20, 25, … Alle disse tal er naturligvis ikke lig med tallet 0. F.eks. er 5 jo ikke lig med 10. Men tallene 5, 10, 15, 20, 25, … er alle kongruente med tallet 0.
\[5 \equiv 0 \:,\: 10 \equiv 0 \:,\: 15 \equiv 0 \:,\: 20 \equiv 0 \:,\: ... \]
Det er klart, at alle hele tal er kongruente med ét af tallene 0, 1, 2, 3, 4. Tænk nemlig på et tal. Vi kan så fortsætte tabellen øverst i det uendelige, og på et eller andet tidspunkt så vil vi nå frem til det tal du tænker på. Øverst i den søjle hvor dette tal står, finder vi et af tallene 0, 1, 2, 3, 4. Det tal, du tænkte på, er så kongruent med tallet i første række, lodret over dit tal.
Negative tal, som -117, er også kongruent med et af tallene 0, 1, 2, 3, 4. Tabellen skal bare fortsættes i negativ retning, og på et eller andet tidspunkt støder vi på tallet -117.
Et tal som 2177 er også kongruent med ét af tallene 0, 1, 2, 3, 4. Men hvilket? Hvis vi ikke vil udfylde tabellen indtil vi når tallet 2177, hvad gør vi så? Lad os se på en del af tabellen fra før:
| 0 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 |
Vi kan skrive alle tal der er større end 4 på en anden måde:
| 0 | 1 | 2 | 3 | 4 |
| \[1 \cdot 5 + 0\] | \[1 \cdot 5 + 1\] | \[1 \cdot 5 + 2\] | \[1 \cdot 5 + 3\] | \[1 \cdot 5 + 4\] |
| \[2 \cdot 5 + 0\] | \[2 \cdot 5 + 1\] | \[2 \cdot 5 + 2\] | \[2 \cdot 5 + 3\] | \[2 \cdot 5 + 4\] |
| \[3 \cdot 5 + 0\] | \[3 \cdot 5 + 1\] | \[3 \cdot 5 + 2\] | \[3 \cdot 5 + 3\] | \[3 \cdot 5 + 4\] |
Vi lægger mærke til, at
– alle tal i kolonnen med et 0 øverst kan skrives som et helt tal gange 5.
– alle tal i kolonnen med et 1-tal øverst kan skrives som et helt tal gange 5, plus 1.
– alle tal i kolonnen med et 2-tal øverst kan skrives som et helt tal gange 5, plus 2.
– alle tal i kolonnen med et 3-tal øverst kan skrives som et helt tal gange 5, plus 3.
– alle tal i kolonnen med et 4-tal øverst kan skrives som et helt tal gange 5, plus 4.
Den opmærksomme læser vil måske genkende regnestykkerne i tabellen herover som noget der kommer fra heltalsdivision.
Hvis vi dividerer f.eks. 17 med 5, så går divisionen ikke op, der kommer en rest på 2:
\[17 = 3 \cdot 5 + 2 \]
Det kan illustreres således:
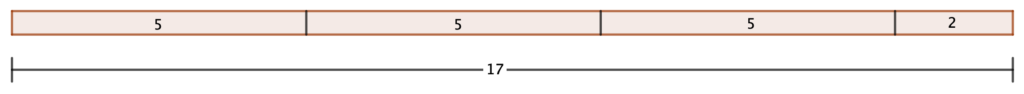
Dermed ser vi at
– alle tal i kolonnen med et 0 øverst giver en rest på 0 ved division med 5.
– alle tal i kolonnen med et 1 øverst giver en rest på 1 ved division med 5.
– alle tal i kolonnen med et 2 øverst giver en rest på 2 ved division med 5.
– alle tal i kolonnen med et 3 øverst giver en rest på 3 ved division med 5.
– alle tal i kolonnen med et 4 øverst giver en rest på 4 ved division med 5.
Her findes forklaringen på begrebet restklasser. Tager man et helt tal, og dividerer det med 5, så får man en rest på 0, 1, 2, 3 eller 4. Resten (ved divisionen) fortæller altså hvilket af tallene 0, 1, 2, 3, 4 som tallet er kongruent med.
Restklassen 0 er de hele tal, så er kongruente med 0. Restklassen 1 er de hele tal, som er kongruente med 1. Restklassen 2 er de hele tal, som er kongruente med 2. Restklassen 3 er de hele tal, som er kongruente med 3. Restklassen 4 er de hele tal, som er kongruente med 4.
En restklasse er altså ikke et tal, men en samling af uendelige mange tal:
\[\bold{0} \;=\; \{... \;,\; -15 \;,\; -10 \;,\; -5 \;,\; 0 \;,\; 5 \;,\; 10 \;,\; 15 \;,\; ...\}\]
\[\bold{1} \;=\; \{... \;,\; -14 \;,\; -9 \;,\; -4 \;,\; 1 \;,\; 6 \;,\; 11 \;,\; 16 \;,\; ...\}\]
\[\bold{2} \;=\; \{... \;,\; -13 \;,\; -8 \;,\; -3 \;,\; 2 \;,\; 7 \;,\; 12 \;,\; 17 \;,\; ...\}\]
\[\bold{3} \;=\; \{... \;,\; -12 \;,\; -7 \;,\; -2 \;,\; 3 \;,\; 8 \;,\; 13 \;,\; 18 \;,\; ...\}\]
\[\bold{4} \;=\; \{... \;,\; -11 \;,\; -6 \;,\; -1 \;,\; 4 \;,\; 9 \;,\; 14 \;,\; 19 \;,\; ...\}\]
Eksempel 1
Lad os finde ud af hvilken restklasse talet 4321 hører til.
Vi dividerer 4321 med 5. Tallet 5 går 864 gange op i 4321, og der er en rest på 1:
\[4321 = 864 \cdot 5 + 1\]
Dermed er \[4321 \equiv 1\], og tallet 4321 hører til restklassen 1.
Eksempel 2
Lad os nu se på kongruens modulo 18.
Antag at vi skal finde du af hvilket af tallene 0, 1, 2, 3, 4, … , 17 som tallet 654321 er kongruent med.
Det er ikke indlysende hvad svaret er. Men lad os dividere 654321 med 18:
\[\frac{654321}{18}=36351.1666667\]
Resultatet fortæller, at 654321 kan skrives som 36351 18’ere, og en rest. Da \[36351 \cdot 18 = 654318\], så mangler vi 3 for at komme helt op til 654321. Vi har altså at
\[654321 = 36351 \cdot 18 + 3\]
Ved divisionen får man en rest på 3, og dermed er 654321 kongruent med 3.
Tallet 654321 hører dermed til restklassen 3 når vi ser på kongruens modulo 18.
